Torus knot
From Wikipedia, the free encyclopedia
A (3,−7)-3D torus knot.
EureleA Award showing a (2,3)-torus knot.
(2,8) torus link
Not to be confused with Torus.
In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q are not coprime (in which case the number of components is gcd(p, q)). A torus knot is trivial (equivalent to the unknot) if and only if either p or q is equal to 1 or −1. The simplest nontrivial example is the (2,3)-torus knot, also known as the trefoil knot.
the (2,−3)-torus knot, also known as the left-handed trefoil knot
Contents
Geometrical representation
A torus knot can be rendered geometrically in multiple ways which are topologically equivalent (see Properties below) but geometrically distinct. The convention used in this article and its figures is the following.The (p,q)-torus knot winds q times around a circle in the interior of the torus, and p times around its axis of rotational symmetry. If p and q are not relatively prime, then we have a torus link with more than one component.
The direction in which the strands of the knot wrap around the torus is also subject to differing conventions. The most common is to have the strands form a right-handed screw for p q > 0.[1][2][3]
The (p,q)-torus knot can be given by the parametrization
 and
and  . This lies on the surface of the torus given by
. This lies on the surface of the torus given by  (in cylindrical coordinates).
(in cylindrical coordinates).Other parameterizations are also possible, because knots are defined up to continuous deformation. The illustrations for the (2,3)- and (3,8)-torus knots can be obtained by taking
 , and in the case of the (2,3)-torus knot by furthermore subtracting respectively
, and in the case of the (2,3)-torus knot by furthermore subtracting respectively  and
and  from the above parameterizations of x and y. The latter generalizes smoothly to any coprime p,q satisfying
from the above parameterizations of x and y. The latter generalizes smoothly to any coprime p,q satisfying  .
.Properties
Diagram of a (3,−8)-torus knot.
Each nontrivial torus knot is prime and chiral.
The (p,q) torus knot is equivalent to the (q,p) torus knot.[1][3] This can be proved by moving the strands on the surface of the torus, which is nicely illustrated here. The (p,−q) torus knot is the obverse (mirror image) of the (p,q) torus knot.[3] The (−p,−q) torus knot is equivalent to the (p,q) torus knot except for the reversed orientation.
The (3, 4) torus knot on the unwrapped torus surface, and its braid word
The crossing number of a (p,q) torus knot with p,q > 0 is given by
- c = min((p−1)q, (q−1)p).
Let Y be the p-fold dunce cap with a disk removed from the interior, Z be the q-fold dunce cap with a disk removed its interior, and X be the quotient space obtained by identifying Y and Z along their boundary circle. The knot complement of the (p, q) -torus knot deformation retracts to the space X. Therefore, the knot group of a torus knot has the presentation
 in the presentation above).
in the presentation above).Connection to complex hypersurfaces
The (p,q)−torus knots arise when considering the link of an isolated complex hypersurface singularity. One intersects the complex hypersurface with a hypersphere, centred at the isolated singular point, and with sufficiently small radius so that it does not enclose, nor encounter, any other singular points. The intersection gives a submanifold of the hypersphere.Let p and q be coprime integers, greater than or equal to two. Consider the holomorphic function
 given by
given by  Let
Let  be the set of
be the set of  such that
such that  Given a real number
Given a real number  we define the real three-sphere
we define the real three-sphere  as given by
as given by  The function
The function  has an isolated critical point at
has an isolated critical point at  since
since  if and only if
if and only if  Thus, we consider the structure of
Thus, we consider the structure of 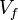 close to
close to  In order to do this, we consider the intersection
In order to do this, we consider the intersection  This intersection is the so-called link of the singularity
This intersection is the so-called link of the singularity  The link of
The link of  , where p and q are coprime, and both greater than or equal to two, is exactly the (p,q)−torus knot.[7]
, where p and q are coprime, and both greater than or equal to two, is exactly the (p,q)−torus knot.[7]











No comments:
Post a Comment