Icosahedral symmetry

From Wikipedia, the free encyclopedia

Point groups in three dimensions
Polyhedral group, [n,3], (*n32)
Involutional symmetry C_s, (*) [ ] =	Cyclic symmetry C_nv, (*nn) [n] =	Dihedral symmetry D_nh, (*n22) [n,2] =
Tetrahedral symmetry T_d, (*332) [3,3] =	Octahedral symmetry O_h, (*432) [4,3] =	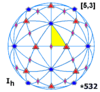Icosahedral symmetry I_h, (*532) [5,3] =

Icosahedral symmetry fundamental domains

A Soccer ball, a common example of a spherical truncated icosahedron, has full icosahedral symmetry.

A regular icosahedron has 60 rotational (or orientation-preserving) symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation. A regular dodecahedron has the same set of symmetries, since it is the dual of the icosahedron.
The set of orientation-preserving symmetries forms a group referred to as A₅ (the alternating group on 5 letters), and the full symmetry group (including reflections) is the product A₅ × Z₂. The latter group is also known as the Coxeter group H₃, and is also represented by Coxeter notation, [5,3] and Coxeter diagram

As point group

Apart from the two infinite series of prismatic and antiprismatic symmetry, rotational icosahedral symmetry or chiral icosahedral symmetry of chiral objects and full icosahedral symmetry or achiral icosahedral symmetry are the discrete point symmetries (or equivalently, symmetries on the sphere) with the largest symmetry groups.
Icosahedral symmetry is not compatible with translational symmetry, so there are no associated crystallographic point groups or space groups.

Schö.	Coxeter		Orb.	Abstract structure	Order
I	[5,3]⁺		532	A₅×2	60
I_h	[5,3]		*532	A₅	120

Presentations corresponding to the above are:

I: \langle s,t \mid s^2, t^3, (st)^5 \rangle\

I_h: \langle s,t\mid s^3(st)^{-2}, t^5(st)^{-2}\rangle.\

These correspond to the icosahedral groups (rotational and full) being the (2,3,5) triangle groups.
The first presentation was given by William Rowan Hamilton in 1856, in his paper on icosian calculus.^[1]
Note that other presentations are possible, for instance as an alternating group (for I).

Visualizations

Schoe. (Orb.)	Coxeter notation	Elements	Mirror diagrams
Schoe. (Orb.)	Coxeter notation	Elements	Orthogonal	Stereographic projection
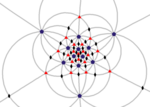
I_h (*532)	[5,3]	Mirror lines: 15
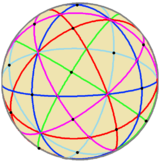
I (532)	[5,3]⁺	Gyration points: 12₅ 20₃ 30₂

Group structure


The edges of a spherical compound of five octahedra represent the 15 mirror planes. Each octahedron can represent 3 orthogonal mirror planes by its edges.

The icosahedral rotation group I is of order 60. The group I is isomorphic to A₅, the alternating group of even permutations of five objects. This isomorphism can be realized by I acting on various compounds, notably the compound of five cubes (which inscribe in the dodecahedron), the compound of five octahedra, or either of the two compounds of five tetrahedra (which are enantiomorphs, and inscribe in the dodecahedron).
The group contains 5 versions of T_h with 20 versions of D₃ (10 axes, 2 per axis), and 6 versions of D₅.
The full icosahedral group I_h has order 120. It has I as normal subgroup of index 2. The group I_h is isomorphic to I × Z₂, or A₅ × Z₂, with the inversion in the center corresponding to element (identity,-1), where Z₂ is written multiplicatively.
I_h acts on the compound of five cubes and the compound of five octahedra, but −1 acts as the identity (as cubes and octahedra are centrally symmetric). It acts on the compound of ten tetrahedra: I acts on the two chiral halves (compounds of five tetrahedra), and −1 interchanges the two halves. Notably, it does not act as S₅, and these groups are not isomorphic; see below for details.
The group contains 10 versions of D_3d and 6 versions of D_5d (symmetries like antiprisms).
I is also isomorphic to PSL₂(5), but I_h is not isomorphic to SL₂(5).

Commonly confused groups

The following groups all have order 120, but are not isomorphic:

S₅, the symmetric group on 5 elements
I_h, the full icosahedral group (subject of this article, also known as H₃)
2I, the binary icosahedral group

They correspond to the following short exact sequences (which do not split) and product

1\to A_5 \to S_5 \to Z_2 \to 1

I_h = A_5 \times Z_2

1\to Z_2 \to 2I\to A_5 \to 1

In words,

$A_5$ is a normal subgroup of $S_5$
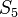
$A_5$ is a factor of $I_h$ , which is a direct product
$A_5$ is a quotient group of $2I$

Note that

A_5

has an exceptional irreducible 3-dimensional representation (as the icosahedral rotation group), but

S_5

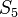does not have an irreducible 3-dimensional representation, corresponding to the full icosahedral group not being the symmetric group.
These can also be related to linear groups over the finite field with five elements, which exhibit the subgroups and covering groups directly; none of these are the full icosahedral group:

$A_5 \cong \operatorname{PSL}(2,5),$ the projective special linear group, see here for a proof;
$S_5 \cong \operatorname{PGL}(2,5),$ the projective general linear group;
$2I \cong \operatorname{SL}(2,5),$ the special linear group.

Conjugacy classes

conjugacy classes
I	I_h
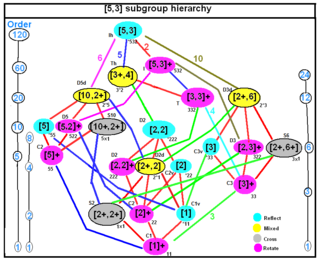
identity 12 × rotation by 72°, order 5 12 × rotation by 144°, order 5 20 × rotation by 120°, order 3 15 × rotation by 180°, order 2	inversion 12 × rotoreflection by 108°, order 10 12 × rotoreflection by 36°, order 10 20 × rotoreflection by 60°, order 6 15 × reflection, order 2

Subgroups of full icosahedral symmetry

Subgroup relations

Chiral subgroup relations

Scho.	Coxeter	Orb.	H-M	Structure	Order	Index
I_h	[5,3]	*532	532/m	A₅×2	120	1
D_2h	[2,2]	*222	mmm	Dih₂×Dih₁=Dih₁³	8	15
C_5v	[5]	*55	5m	Dih₅	10	12
C_3v	[3]	*33	3m	Dih₃=S₃	6	20
C_2v	[2]	*22	mm2	Dih₂=Dih₁²	4	30
C_s	[ ]	*	2 or m	Dih₁	2	60
T_h	[3⁺,4]	3*2	m3	A₄×2	24	5
D_5d	[2⁺,10]	2*5	10m2	Dih₁₀=Z₂×Dih₅	20	6
D_3d	[2⁺,6]	2*3	3m	Dih₆=Z₂×Dih₃	12	10
D_1d = C_2h	[2⁺,2]	2*	2/m	Dih₂=Z₂×Dih₁	4	30
S₁₀	[2⁺,10⁺]	5×	5	Z₁₀=Z₂×Z₅	10	12
S₆	[2⁺,6⁺]	3×	3	Z₆=Z₂×Z₃	6	20
S₂	[2⁺,2⁺]	×	1	Z₂	2	60
I	[5,3]⁺	532	532	A₅	60	2
T	[3,3]⁺	332	332	A₄	12	10
D₅	[2,5]⁺	225	225	Dih₅	10	12
D₃	[2,3]⁺	223	223	Dih₃=S₃	6	20
D₂	[2,2]⁺	222	222	Dih₂=Z₂²	4	30
C₅	[5]⁺	55	5	Z₅	5	24
C₃	[3]⁺	33	3	Z₃=A₃	3	40
C₂	[2]⁺	22	2	Z₂	2	60
C₁	[ ]⁺	11	1	Z₁	1	120

All of these classes of subgroups are conjugate (i.e., all vertex stabilizers are conjugate), and admit geometric interpretations.
Note that the stabilizer of a vertex/edge/face/polyhedron and its opposite are equal, since

-1

is central.

Vertex stabilizers

Stabilizers of an opposite pair of vertices can be interpreted as stabilizers of the axis they generate.

vertex stabilizers in I give cyclic groups C₃
vertex stabilizers in I_h give dihedral groups D₃
stabilizers of an opposite pair of vertices in I give dihedral groups D₃
stabilizers of an opposite pair of vertices in I_h give $D_3 \times \pm 1$

Edge stabilizers

Stabilizers of an opposite pair of edges can be interpreted as stabilizers of the rectangle they generate.

edges stabilizers in I give cyclic groups Z₂
edges stabilizers in I_h give Klein four-groups $Z_2 \times Z_2$
stabilizers of a pair of edges in I give Klein four-groups $Z_2 \times Z_2$ ; there are 5 of these, given by rotation by 180° in 3 perpendicular axes.
stabilizers of a pair of edges in I_h give $Z_2 \times Z_2 \times Z_2$ ; there are 5 of these, given by reflections in 3 perpendicular axes.

Face stabilizers

Stabilizers of an opposite pair of faces can be interpreted as stabilizers of the anti-prism they generate.

face stabilizers in I give cyclic groups C₅
face stabilizers in I_h give dihedral groups D₅
stabilizers of an opposite pair of faces in I give dihedral groups D₅
stabilizers of an opposite pair of faces in I_h give $D_5 \times \pm 1$

Polyhedron stabilizers

For each of these, there are 5 conjugate copies, and the conjugation action gives a map, indeed an isomorphism,

I \stackrel{\sim}\to A_5 < S_5

stabilizers of the inscribed tetrahedra in I are a copy of T
stabilizers of the inscribed tetrahedra in I_h are a copy of T_h
stabilizers of the inscribed cubes (or opposite pair of tetrahedra, or octahedrons) in I are a copy of O
stabilizers of the inscribed cubes (or opposite pair of tetrahedra, or octahedrons) in I_h are a copy of O_h

Fundamental domain

Fundamental domains for the icosahedral rotation group and the full icosahedral group are given by:

Icosahedral rotation group I	Full icosahedral group I_h	Faces of disdyakis triacontahedron are the fundamental domain

In the disdyakis triacontahedron one full face is a fundamental domain; other solids with the same symmetry can be obtained by adjusting the orientation of the faces, e.g. flattening selected subsets of faces to combine each subset into one face, or replacing each face by multiple faces, or a curved surface.

Solids with icosahedral symmetry

For more details on this topic, see Solids with icosahedral symmetry.

Chiral solids

Class	Name	picture	Faces	Edges	Vertices
Archimedean solid	snub dodecahedron		92	150	60
Catalan solid	pentagonal hexecontahedron		60	50	92

Full icosahedral symmetry

Platonic solids
{5,3}	{3,5}
Archimedean solids
3.10.10	4.6.10	5.6.6	3.4.5.4	3.5.3.5
Catalan solids
V3.10.10	V4.6.10	V5.6.6	V3.4.5.4	V3.5.3.5

Other objects with icosahedral symmetry

Icosahedral capsid of an Adenovirus

This section requires expansion. (January 2010)

Barth surfaces
Virus structure, and Capsid

Liquid crystals with icosahedral symmetry

For the intermediate material phase called liquid crystals the existence of icosahedral symmetry was proposed by H. Kleinert and K. Maki^[2] and its structure was first analyzed in detail in that paper. See the review article here. In aluminum, the icosahedral structure was discovered experimentally three years after this by Dan Shechtman, which earned him the Nobel Prize in 2011.

Related geometries

Icosahedral symmetry is equivalently the projective special linear group PSL(2,5), and is the symmetry group of the modular curve X(5), and more generally PSL(2,p) is the symmetry group of the modular curve X(p). The modular curve X(5) is geometrically a dodecahedron with a cusp at the center of each polygonal face, which demonstrates the symmetry group.
This geometry, and associated symmetry group, was studied by Felix Klein as the monodromy groups of a Belyi surface – a Riemann surface with a holomorphic map to the Riemann sphere, ramified only at 0, 1, and infinity (a Belyi function) – the cusps are the points lying over infinity, while the vertices and the centers of each edge lie over 0 and 1; the degree of the covering (number of sheets) equals 5.
This arose from his efforts to give a geometric setting for why icosahedral symmetry arose in the solution of the quintic equation, with the theory given in the famous (Klein 1888); a modern exposition is given in (Tóth 2002, Section 1.6, Additional Topic: Klein's Theory of the Icosahedron, p. 66).
Klein's investigations continued with his discovery of order 7 and order 11 symmetries in (Klein 1878/79b) and (Klein 1879) (and associated coverings of degree 7 and 11) and dessins d'enfants, the first yielding the Klein quartic, whose associated geometry has a tiling by 24 heptagons (with a cusp at the center of each).
Similar geometries occur for PSL(2,n) and more general groups for other modular curves.
More exotically, there are special connections between the groups PSL(2,5) (order 60), PSL(2,7) (order 168) and PSL(2,11) (order 660), which also admit geometric interpretations – PSL(2,5) is the symmetries of the icosahedron (genus 0), PSL(2,7) of the Klein quartic (genus 3), and PSL(2,11) the buckyball surface (genus 70). These groups form a "trinity" in the sense of Vladimir Arnold, which gives a framework for the various relationships; see trinities for details.
There is a close relationship to other Platonic solids.

Mathematics

Sunday, 1 November 2015