Tensor algebra
From Wikipedia, the free encyclopedia
In mathematics, the tensor algebra of a vector space V, denoted T(V) or T •(V), is the algebra of tensors on V (of any rank) with multiplication being the tensor product. It is the free algebra on V, in the sense of being left adjoint to the forgetful functor from algebras to vector spaces: it is the "most general" algebra containing V, in the sense of the corresponding universal property (see below).
The tensor algebra also has two coalgebra structures; one simple one, which does not make it a bialgebra, and a more complicated one, which yields a bialgebra, and can be extended with an antipode to a Hopf algebra structure.
Note: In this article, all algebras are assumed to be unital and associative.
The tensor algebra also has two coalgebra structures; one simple one, which does not make it a bialgebra, and a more complicated one, which yields a bialgebra, and can be extended with an antipode to a Hopf algebra structure.
Note: In this article, all algebras are assumed to be unital and associative.
Contents
Construction
Let V be a vector space over a field K. For any nonnegative integer k, we define the kth tensor power of V to be the tensor product of V with itself k times:We then construct T(V) as the direct sum of TkV for k = 0,1,2,…
 for negative integers k.
for negative integers k.The construction generalizes in straightforward manner to the tensor algebra of any module M over a commutative ring. If R is a non-commutative ring, one can still perform the construction for any R-R bimodule M. (It does not work for ordinary R-modules because the iterated tensor products cannot be formed.)
Adjunction and universal property
The tensor algebra T(V) is also called the free algebra on the vector space V, and is functorial. As with other free constructions, the functor T is left adjoint to some forgetful functor. In this case, it's the functor which sends each K-algebra to its underlying vector space.Explicitly, the tensor algebra satisfies the following universal property, which formally expresses the statement that it is the most general algebra containing V:
- Any linear transformation f : V → A from V to an algebra A over K can be uniquely extended to an algebra homomorphism from T(V) to A as indicated by the following commutative diagram:
The above universal property shows that the construction of the tensor algebra is functorial in nature. That is, T is a functor from the K-Vect, category of vector spaces over K, to K-Alg, the category of K-algebras. The functoriality of T means that any linear map from V to W extends uniquely to an algebra homomorphism from T(V) to T(W).
Non-commutative polynomials
If V has finite dimension n, another way of looking at the tensor algebra is as the "algebra of polynomials over K in n non-commuting variables". If we take basis vectors for V, those become non-commuting variables (or indeterminants) in T(V), subject to no constraints beyond associativity, the distributive law and K-linearity.Note that the algebra of polynomials on V is not
 , but rather
, but rather  : a (homogeneous) linear function on V is an element of
: a (homogeneous) linear function on V is an element of  for example coordinates
for example coordinates  on a vector space are covectors, as they take in a vector and give out a scalar (the given coordinate of the vector).
on a vector space are covectors, as they take in a vector and give out a scalar (the given coordinate of the vector).Quotients
Because of the generality of the tensor algebra, many other algebras of interest can be constructed by starting with the tensor algebra and then imposing certain relations on the generators, i.e. by constructing certain quotient algebras of T(V). Examples of this are the exterior algebra, the symmetric algebra, Clifford algebras and universal enveloping algebras.Coalgebra structures
The tensor algebra has two coalgebra structures; one simple one, which does not make it a bialgebra, and a more complicated one, which yields a bialgebra, and can be extended with an antipode to a Hopf algebra structure.Simple coalgebra structure
The simple coalgebra structure on the tensor algebra is given as follows. The coproduct Δ is defined by for every
for every  and
and for every
for every  for every
for every  .
.
The tensor algebra is not a bialgebra with this coproduct.
Bialgebra and Hopf algebra structure
However, the following more complicated coproduct does yield a bialgebra:Finally, the tensor algebra becomes a Hopf algebra with antipode given by
This is just the standard Hopf algebra structure on a free algebra, where one defines the comultiplication on
 by
by via
via by
by with this property, i.e. we define the antipode on
with this property, i.e. we define the antipode on  via
via







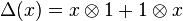



No comments:
Post a Comment