Spin wave
From Wikipedia, the free encyclopedia
(Redirected from Spin waves)
Spin waves are propagating disturbances in the ordering of magnetic materials. These low-lying
collective excitations occur in magnetic lattices with
continuous symmetry. From the equivalent quasiparticle point of view, spin waves are known as
magnons, which are boson modes of the spin lattice that correspond roughly to the
phonon excitations of the nuclear lattice. As temperature is increased, the thermal excitation of spin waves reduces a
ferromagnet's spontaneous magnetization. The energies of spin waves are typically only
μeV in keeping with typical
Curie points at room temperature and below. The discussion of spin waves in
antiferromagnets is beyond the scope of this article.
Theory
An illustration of the precession of a spin wave about an applied
magnetic field with a wavelength that is eleven times the lattice
constant.
The projection of the magnetization of the same spin wave along the
chain direction as a function of distance along the spin chain.
The simplest way of understanding spin waves is to consider the
Hamiltonian 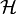
for the
Heisenberg ferromagnet:

where
J is the
exchange energy, the operators
S represent the
spins at
Bravais lattice points,
g is the
Landé g-factor,
μB is the
Bohr magneton and
H
is the internal field which includes the external field plus any
"molecular" field. Note that in the classical continuum case and in
1 + 1 dimensions
Heisenberg ferromagnet equation has the form

In
1 + 1, 2 + 1 and
3 + 1 dimensions this equation admits several integrable and non-integrable extensions like the
Landau-Lifshitz equation, the
Ishimori equation and so on. For a ferromagnet
J > 0 and the ground state of the Hamiltonian

is that in which all spins are aligned parallel with the field
H. That

is an eigenstate of
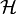
can be verified by rewriting it in terms of the spin-raising and spin-lowering operators given by:

resulting in

where
z has been taken as the direction of the magnetic field. The spin-lowering operator
S− annihilates the state with minimum projection of spin along the
z-axis, while the spin-raising operator
S+ annihilates the ground state with maximum spin projection along the
z-axis. Since

for the maximally aligned state, we find

where N is the total number of Bravais lattice sites. The proposition
that the ground state is an eigenstate of the Hamiltonian is confirmed.
One might guess that the first excited state of the Hamiltonian has one randomly selected spin at position
i rotated so that

but in fact this arrangement of spins is not an eigenstate. The
reason is that such a state is transformed by the spin raising and
lowering operators. The operator

will increase the
z-projection of the spin at position
i back to its low-energy orientation, but the operator

will lower the
z-projection of the spin at position
j.
The combined effect of the two operators is therefore to propagate the
rotated spin to a new position, which is a hint that the correct
eigenstate is a
spin wave, namely a superposition of states with
one reduced spin. The exchange energy penalty associated with changing
the orientation of one spin is reduced by spreading the disturbance over
a long wavelength. The degree of misorientation of any two
near-neighbor spins is thereby minimized. From this explanation one can
see why the
Ising model magnet with
discrete symmetry
has no spin waves: the notion of spreading a disturbance in the spin
lattice over a long wavelength makes no sense when spins have only two
possible orientations. The existence of low-energy excitations is
related to the fact that in the absence of an external field, the spin
system has an infinite number of degenerate ground states with
infinitesimally different spin orientations. The existence of these
ground states can be seen from the fact that the state

does not have the full rotational symmetry of the Hamiltonian
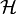
, a phenomenon which is called
spontaneous symmetry breaking.
In this model the magnetization
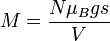
where
V is the volume. The propagation of spin waves is described by the Landau-Lifshitz equation of motion:

where
γ is the gyromagnetic ratio and
λ
is the damping constant. The cross-products in this forbidding-looking
equation show that the propagation of spin waves is governed by the
torques generated by internal and external fields. (An equivalent form
is the
Landau-Lifshitz-Gilbert equation, which replaces the final term by a more "simply looking" equivalent one.)
The first term on the r.h.s. describes the precession of the
magnetization under the influence of the applied field, while the
above-mentioned final term describes how the magnetization vector
"spirals in" towards the field direction as time progresses. In metals
the damping forces described by the constant
λ are in many cases dominated by the eddy currents.
One important difference between phonons and magnons lies in their
dispersion relations. The dispersion relation for phonons is to first order linear in wavevector
k, namely
ώ = ck, where
ω is frequency, and
c is the velocity of sound. Magnons have a parabolic dispersion relation:
ώ = Ak2 where the parameter
A represents a "
spin stiffness." The
k2 form is the third term of a Taylor expansion of a cosine term in the energy expression originating from the
Si ⋅ Sj dot-product. The underlying reason for the difference in dispersion relation is that ferromagnets violate
time-reversal symmetry. Two adjacent spins in a solid with lattice constant
a that participate in a mode with wavevector
k have an angle between them equal to
ka.
Experimental observation
Spin waves are observed through four experimental methods: inelastic
neutron scattering, inelastic
light scattering (
Brillouin scattering,
Raman scattering and inelastic
X-ray scattering), inelastic electron scattering (spin-resolved
electron energy loss spectroscopy), and spin-wave resonance (
ferromagnetic resonance).
In the first method the energy loss of a beam of neutrons that excite a
magnon is measured, typically as a function of scattering vector (or
equivalently momentum transfer), temperature and external magnetic
field. Inelastic neutron scattering measurements can determine the
dispersion curve for magnons just as they can for
phonons. Important inelastic neutron scattering facilities are present at the
ISIS neutron source in Oxfordshire, UK, the
Institut Laue-Langevin in
Grenoble, France, the
High Flux Isotope Reactor at
Oak Ridge National Laboratory in Tennessee, USA, and at the
National Institute of Standards and Technology in Maryland, USA. Brillouin scattering similarly measures the energy loss of
photons
(usually at a convenient visible wavelength) reflected from or
transmitted through a magnetic material. Brillouin spectroscopy is
similar to the more widely known
Raman scattering
but probes a lower energy and has a higher energy resolution in order
to be able to detect the meV energy of magnons. Ferromagnetic (or
antiferromagnetic) resonance instead measures the absorption of
microwaves,
incident on a magnetic material, by spin waves, typically as a function
of angle, temperature and applied field. Ferromagnetic resonance is a
convenient laboratory method for determining the effect of
magnetocrystalline anisotropy on the dispersion of spin waves. Very recently, one group in
Max Planck Institute for Microstructure Physics in Halle Germany proved that by using
spin polarized electron energy loss spectroscopy (SPEELS),
very high energy surface magnons can be excited. This technique allows
people for the first time to probe the dispersion of magnons in the
ultrathin ferromagnetic films. The first experiment was performed for a 5
ML Fe film.
[1]
With momentum resolution, the magnon dispersion was explored for an 8
ML fcc Co film on Cu(001) and an 8 ML hcp Co on W(110), respectively.
[2] The maximum magnon energy at the border of the surface Brillouin zone was 240 meV.
Practical significance
When magnetoelectronic devices are operated at high frequencies, the
generation of spin waves can be an important energy loss mechanism. Spin
wave generation limits the linewidths and therefore the
quality factors Q of
ferrite components used in
microwave
devices. The reciprocal of the lowest frequency of the characteristic
spin waves of a magnetic material gives a time scale for the switching
of a device based on that material.
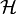 for the Heisenberg ferromagnet:
for the Heisenberg ferromagnet: is that in which all spins are aligned parallel with the field H. That
is that in which all spins are aligned parallel with the field H. That  is an eigenstate of
is an eigenstate of 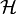 can be verified by rewriting it in terms of the spin-raising and spin-lowering operators given by:
can be verified by rewriting it in terms of the spin-raising and spin-lowering operators given by: will increase the z-projection of the spin at position i back to its low-energy orientation, but the operator
will increase the z-projection of the spin at position i back to its low-energy orientation, but the operator  will lower the z-projection of the spin at position j.
The combined effect of the two operators is therefore to propagate the
rotated spin to a new position, which is a hint that the correct
eigenstate is a spin wave, namely a superposition of states with
one reduced spin. The exchange energy penalty associated with changing
the orientation of one spin is reduced by spreading the disturbance over
a long wavelength. The degree of misorientation of any two
near-neighbor spins is thereby minimized. From this explanation one can
see why the Ising model magnet with discrete symmetry
has no spin waves: the notion of spreading a disturbance in the spin
lattice over a long wavelength makes no sense when spins have only two
possible orientations. The existence of low-energy excitations is
related to the fact that in the absence of an external field, the spin
system has an infinite number of degenerate ground states with
infinitesimally different spin orientations. The existence of these
ground states can be seen from the fact that the state
will lower the z-projection of the spin at position j.
The combined effect of the two operators is therefore to propagate the
rotated spin to a new position, which is a hint that the correct
eigenstate is a spin wave, namely a superposition of states with
one reduced spin. The exchange energy penalty associated with changing
the orientation of one spin is reduced by spreading the disturbance over
a long wavelength. The degree of misorientation of any two
near-neighbor spins is thereby minimized. From this explanation one can
see why the Ising model magnet with discrete symmetry
has no spin waves: the notion of spreading a disturbance in the spin
lattice over a long wavelength makes no sense when spins have only two
possible orientations. The existence of low-energy excitations is
related to the fact that in the absence of an external field, the spin
system has an infinite number of degenerate ground states with
infinitesimally different spin orientations. The existence of these
ground states can be seen from the fact that the state  does not have the full rotational symmetry of the Hamiltonian
does not have the full rotational symmetry of the Hamiltonian 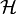 , a phenomenon which is called spontaneous symmetry breaking.
, a phenomenon which is called spontaneous symmetry breaking.








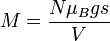

No comments:
Post a Comment