Sunday, 1 November 2015

Teltron tube

Teltron tube

From Wikipedia, the free encyclopedia
Teltron electron beam tube
Teltron diffraction tube with Helmholtz coils and stand
A teltron tube (named for Teltron Inc., which is now owned by 3B Scientific Ltd.) is a type of cathode ray tube used to demonstrate the properties of electrons. It usually contains two electron guns, which can project two thin electron beams at right angles. The beams can be bent by applying voltages to various electrodes in the tube. The electron beams are visible as fine bluish lines. This is accomplished by filling the tube with low pressure helium (He) or Hydrogen (H2) gas. A few of the electrons in the beam collide with the helium atoms, causing them to fluoresce and emit light.
They are usually used to teach electromagnetic effects because they show how an electron beam is affected by electric fields and by magnetic fields like the Lorentz force.

Contents

Motions in fields

Charged particles in a uniform electric field follow a parabolic trajectory, since the electric field term (of the Lorentz force which acts on the particle) is the product of the particle's charge and the magnitude of the electric field, (oriented in the direction of the electric field). In a uniform magnetic field however, charged particles follow a circular trajectory due to the cross product in the magnetic field term of the Lorentz force. (That is, the force from the magnetic field acts on the particle in a direction perpendicular to the particle's direction of motion. See: Lorentz force for more details.)

Apparatus

The 'teltron' apparatus consists of a Teltron type electron deflection tube, a Teltron stand, EHT power supply (0 - 5000 V DC, variable).

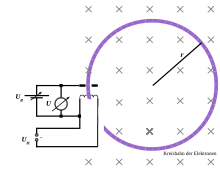
Experimental setup

Experimental sketch fine beam
In an evacuated glass bulb some hydrogen gas (H2) is filled, so that the tube has a hydrogen atmosphere at low pressure of about 1 Pa is formed. The pressure is such that the electrons are decelerated by collisions as little as possible (change in kinetic energy), the number of collisions are few but sufficient to emit visible light. Inside the bulb there is an electron gun. This consists of a heating spiral, a cathode and an anode hole. From the cathode (-) electrons are emitted and accelerated by the electric field towards the positively charged anode (+). Through a hole in the anode, the electrons leave the beam forming system and the Wehnelt cylinder bundles.

Results

Another experimental setup showing the electron beam orbit
When the heater is energized, the heating coil will cause electrons to emerge from it due to thermionic emission. In the electric field between anode and cathode, the electric field acts on the electrons, which accelerate to a high velocity, such that the electrons leave through a small opening in the anode as an electron beam. Only when the coil current is turned on will a force act on the beam and change its direction. Otherwise it will retain its velocity. If, however, the coil current is switched on, the Lorentz force will direct the electrons into a circular orbit.

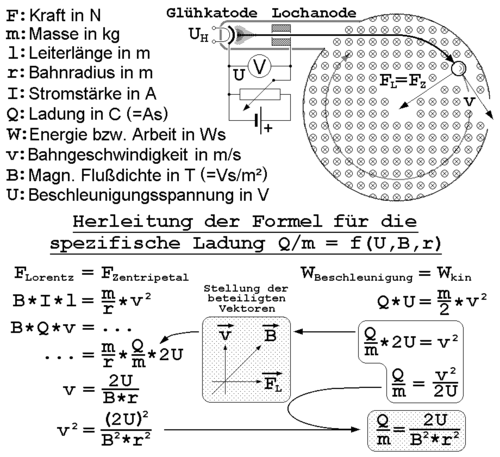
Determination of the specific electron charge

Derivation of the formula to determine the specific charge of the electron with the help of the filament beam-test
The higher the coil current, the stronger magnetic field and thus smaller radius of the circular path of the electrons. The strength of the magnetic field and the Lorentz force are proportional to each other, such that when the Lorentz force increases. A larger Lorentz force will deflect the electrons more strongly, so the orbit will be smaller. The Lorentz force F_L is always perpendicular to the instantaneous direction of movement and allows a centripetal F_Z circular motion. The magnitude of the velocity and hence the kinetic energy can not change:
\begin{align} F_L &= F_Z\\ e\cdot v\cdot B &= m\cdot\frac{v^2}{r} \end{align}
From this we get the amount of specific electron charge
\frac{e}{m} = \frac{v}{B\cdot r}
The determination of the velocity is performed using the energy conservation law
e\cdot U = \frac{1}{2}\cdot m\cdot v^2
This is finally followed by
\frac{e}{m} = \frac{2 \, U}{r^2\cdot B^2}
The specific electron charge has the value
\frac{-e}{m} \approx -1{.}7588202 \cdot 10^{11} \, \mathrm{\frac{C}{kg}}
Since the charge of an electron is available from the Millikan experiment, the study of electrons in an magnetic field is the determination of its mass in accordance with:
\ m = \frac{e \cdot r^2 \cdot B^2}{2 \, U} \approx 9{.}1094 \cdot 10^{-31} \, \mathrm{kg}
Similar concepts for the weighing of charged particles can be found in the mass spectrometer.

External links

Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)