Matrix multiplication
From Wikipedia, the free encyclopedia
(Redirected from Frobenius inner product)
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. Numbers such as the real or complex numbers can be multiplied according to elementary arithmetic. On the other hand, matrices are arrays of numbers,
so there is no unique way to define "the" multiplication of matrices.
As such, in general the term "matrix multiplication" refers to a number
of different ways to multiply matrices. The key features of any matrix
multiplication include: the number of rows and columns the original
matrices have (called the "size", "order" or "dimension"), and specifying how the entries of the matrices generate the new matrix.
Like vectors, matrices of any size can be multiplied by scalars, which amounts to multiplying every entry of the matrix by the same number. Similar to the entrywise definition of adding or subtracting matrices, multiplication of two matrices of the same size can be defined by multiplying the corresponding entries, and this is known as the Hadamard product. Another definition is the Kronecker product of two matrices, to obtain a block matrix.
One can form many other definitions. However, the most useful definition can be motivated by linear equations and linear transformations on vectors, which have numerous applications in applied mathematics, physics, and engineering. This definition is often called the matrix product.[1][2] In words, if A is an n × m matrix and B is an m × p matrix, their matrix product AB is an n × p matrix, in which the m entries across the rows of A are multiplied with the m entries down the columns of B (the precise definition is below).
This definition is not commutative, although it still retains the associative property and is distributive over entrywise addition of matrices. The identity element of the matrix product is the identity matrix (analogous to multiplying numbers by 1), and a square matrix may have an inverse matrix (analogous to the multiplicative inverse of a number). A consequence of the matrix product is determinant multiplicativity. The matrix product is an important operation in linear transformations, matrix groups, and the theory of group representations and irreps.
Computing matrix products is both a central operation in many numerical algorithms and potentially time consuming, making it one of the most well-studied problems in numerical computing. Various algorithms have been devised for computing C = AB, especially for large matrices.
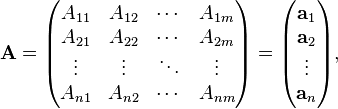
This article will use the following notational conventions: matrices are represented by capital letters in bold, e.g. A, vectors in lowercase bold, e.g. a, and entries of vectors and matrices are italic (since they are scalars), e.g. A and a. Index notation is often the clearest way to express definitions, and is used as standard in the literature. The i, j entry of matrix A is indicated by (A)ij or Aij, whereas a numerical label (not matrix entries) on a collection of matrices is subscripted only, e.g. A1, A2, etc.
Like vectors, matrices of any size can be multiplied by scalars, which amounts to multiplying every entry of the matrix by the same number. Similar to the entrywise definition of adding or subtracting matrices, multiplication of two matrices of the same size can be defined by multiplying the corresponding entries, and this is known as the Hadamard product. Another definition is the Kronecker product of two matrices, to obtain a block matrix.
One can form many other definitions. However, the most useful definition can be motivated by linear equations and linear transformations on vectors, which have numerous applications in applied mathematics, physics, and engineering. This definition is often called the matrix product.[1][2] In words, if A is an n × m matrix and B is an m × p matrix, their matrix product AB is an n × p matrix, in which the m entries across the rows of A are multiplied with the m entries down the columns of B (the precise definition is below).
This definition is not commutative, although it still retains the associative property and is distributive over entrywise addition of matrices. The identity element of the matrix product is the identity matrix (analogous to multiplying numbers by 1), and a square matrix may have an inverse matrix (analogous to the multiplicative inverse of a number). A consequence of the matrix product is determinant multiplicativity. The matrix product is an important operation in linear transformations, matrix groups, and the theory of group representations and irreps.
Computing matrix products is both a central operation in many numerical algorithms and potentially time consuming, making it one of the most well-studied problems in numerical computing. Various algorithms have been devised for computing C = AB, especially for large matrices.
This article will use the following notational conventions: matrices are represented by capital letters in bold, e.g. A, vectors in lowercase bold, e.g. a, and entries of vectors and matrices are italic (since they are scalars), e.g. A and a. Index notation is often the clearest way to express definitions, and is used as standard in the literature. The i, j entry of matrix A is indicated by (A)ij or Aij, whereas a numerical label (not matrix entries) on a collection of matrices is subscripted only, e.g. A1, A2, etc.
Contents
- 1 Scalar multiplication
- 2 Matrix product (two matrices)
- 3 Matrix product (any number)
- 4 Operations derived from the matrix product
- 5 Applications of the matrix product
- 6 The inner and outer products
- 7 Algorithms for efficient matrix multiplication
- 8 Other forms of multiplication
- 9 See also
- 10 Notes
- 11 References
- 12 External links
Scalar multiplication
Main article: Scalar multiplication
The simplest form of multiplication associated with matrices is scalar multiplication, which is a special case of the Kronecker product.The left scalar multiplication of a matrix A with a scalar λ gives another matrix λA of the same size as A. The entries of λA are defined by
For a real scalar and matrix:
Matrix product (two matrices)
Assume two matrices are to be multiplied (the generalization to any number is discussed below).General definition of the matrix product
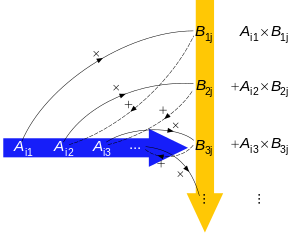
Arithmetic process of multiplying numbers (solid lines) in row i in matrix A and column j in matrix B, then adding the terms (dashed lines) to obtain entry ij in the final matrix.
Usually the entries are numbers or expressions, but can even be matrices themselves (see block matrix). The matrix product can still be calculated exactly the same way. See below for details on how the matrix product can be calculated in terms of blocks taking the forms of rows and columns.
Illustration
The figure to the right illustrates diagrammatically the product of two matrices A and B, showing how each intersection in the product matrix corresponds to a row of A and a column of B.Examples of matrix products
Row vector and column vector
IfSquare matrix and column vector
IfThe product of a square matrix multiplied by a column matrix arises naturally in linear algebra; for solving linear equations and representing linear transformations. By choosing a, b, c, p, q, r, u, v, w in A appropriately, A can represent a variety of transformations such as rotations, scaling and reflections, shears, of a geometric shape in space.
Square matrices
IfRow vector, square matrix, and column vector
IfRectangular matrices
IfProperties of the matrix product (two matrices)
Analogous to numbers (elements of a field), matrices satisfy the following general properties, although there is one subtlety, due to the nature of matrix multiplication.[7][8]All matrices
- Not commutative:
In general:
In index notation:
- Distributive over matrix addition:
Left distributivity:
- Scalar multiplication is compatible with matrix multiplication:
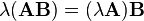 and
and 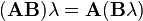
- Transpose:
In index notation:
- Complex conjugate:
If A and B have complex entries, then
In index notation:
- Conjugate transpose:
If A and B have complex entries, then
In index notation:
- Traces:
The trace of a product AB is independent of the order of A and B:
For extensive details on differentials and derivatives of products of matrix functions, see matrix calculus.
Square matrices only
Main article: square matrix
- Identity element:
If A is a square matrix, then
- Inverse matrix:
If A is a square matrix, there may be an inverse matrix A−1 of A such that
- Determinants:
When a determinant of a matrix is defined (i.e., when the underlying ring is commutative), if A and B are square matrices of the same order, the determinant of their product AB equals the product of their determinants:
Matrix product (any number)
Main article: Matrix chain multiplication
Matrix multiplication can be extended to the case of more than two
matrices, provided that for each sequential pair, their dimensions
match.The product of n matrices A1, A2, ..., An with sizes s0 × s1, s1 × s2, ..., sn − 1 × sn (where s0, s1, s2, ..., sn are all simply positive integers and the subscripts are labels corresponding to the matrices, nothing more), is the s0 × sn matrix:
Properties of the matrix product (any number)
The same properties will hold, as long as the ordering of matrices is not changed. Some of the previous properties for more than two matrices generalize as follows.- Associative:
The matrix product is associative. If three matrices A, B, and C are respectively m × p, p × q, and q × r matrices, then there are two ways of grouping them without changing their order, and
If four matrices A, B, C, and D are respectively m × p, p × q, q × r, and r × s matrices, then there are five ways of grouping them without changing their order, and
In general, the number of possible ways of grouping n matrices for multiplication is equal to the (n − 1)th Catalan number - Trace:
The trace of a product of n matrices A1, A2, ..., An is invariant under cyclic permutations of the matrices in the product:
- Determinant:
For square matrices only, the determinant of a product is the product of determinants:
Examples of chain multiplication
Similarity transformations involving similar matrices are matrix products of the three square matrices, in the form:Operations derived from the matrix product
More operations on square matrices can be defined using the matrix product, such as powers and nth roots by repeated matrix products, the matrix exponential can be defined by a power series, the matrix logarithm is the inverse of matrix exponentiation, and so on.Powers of matrices
Square matrices can be multiplied by themselves repeatedly in the same way as ordinary numbers, because they always have the same number of rows and columns. This repeated multiplication can be described as a power of the matrix, a special case of the ordinary matrix product. On the contrary, rectangular matrices do not have the same number of rows and columns so they can never be raised to a power. An n × n matrix A raised to a positive integer k is defined as- Zero power:
- Scalar multiplication:
- Determinant:
A special case is the power of a diagonal matrix. Since the product of diagonal matrices amounts to simply multiplying corresponding diagonal elements together, the power k of a diagonal matrix A will have entries raised to the power. Explicitly;
Applications of the matrix product
Linear transformations
Main article: Linear transformations
Matrices offer a concise way of representing linear transformations between vector spaces, and matrix multiplication corresponds to the composition of linear transformations. The matrix product of two matrices can be defined when their entries belong to the same ring, and hence can be added and multiplied.Let U, V, and W be vector spaces over the same field with given bases, S: V → W and T: U → V be linear transformations and ST: U → W be their composition.
Suppose that A, B, and C are the matrices representing the transformations S, T, and ST with respect to the given bases.
Then AB = C, that is, the matrix of the composition (or the product) of linear transformations is the product of their matrices with respect to the given bases.
Linear systems of equations
A system of linear equations with the same number of equations as variables can be solved by collecting the coefficients of the equations into a square matrix, then inverting the matrix equation.A similar procedure can be used to solve a system of linear differential equations, see also phase plane.
Group theory and representation theory
The inner and outer products
Given two column vectors a and b, the Euclidean inner product and outer product are the simplest special cases of the matrix product.[9]Inner product
The inner product of two vectors in matrix form is equivalent to a column vector multiplied on the left by a row vector:The matrix product itself can be expressed in terms of inner product. Suppose that the first n × m matrix A is decomposed into its row vectors ai, and the second m × p matrix B into its column vectors bi:[1]
Outer product
The outer product (also known as the dyadic product or tensor product) of two vectors in matrix form is equivalent to a row vector multiplied on the left by a column vector:Algorithms for efficient matrix multiplication
Main article: Matrix multiplication algorithm
The bound on ω over time.
 . Strassen's algorithm is more complex, and the numerical stability is reduced compared to the naïve algorithm.[10] Nevertheless, it appears in several libraries, such as BLAS, where it is significantly more efficient for matrices with dimensions n > 100,[11] and is very useful for large matrices over exact domains such as finite fields, where numerical stability is not an issue.
. Strassen's algorithm is more complex, and the numerical stability is reduced compared to the naïve algorithm.[10] Nevertheless, it appears in several libraries, such as BLAS, where it is significantly more efficient for matrices with dimensions n > 100,[11] and is very useful for large matrices over exact domains such as finite fields, where numerical stability is not an issue.The current O(nk) algorithm with the lowest known exponent k is a generalization of the Coppersmith–Winograd algorithm that has an asymptotic complexity of O(n2.3728639), by François Le Gall.[12] This algorithm, and the Coppersmith–Winograd algorithm on which it is based, are similar to Strassen's algorithm: a way is devised for multiplying two k × k-matrices with fewer than k3 multiplications, and this technique is applied recursively. However, the constant coefficient hidden by the Big O notation is so large that these algorithms are only worthwhile for matrices that are too large to handle on present-day computers.[13][14]
Since any algorithm for multiplying two n × n-matrices has to process all 2 × n2-entries, there is an asymptotic lower bound of Ω(n2) operations. Raz (2002) proves a lower bound of Ω(n2 log(n)) for bounded coefficient arithmetic circuits over the real or complex numbers.
Cohn et al. (2003, 2005) put methods such as the Strassen and Coppersmith–Winograd algorithms in an entirely different group-theoretic context, by utilising triples of subsets of finite groups which satisfy a disjointness property called the triple product property (TPP). They show that if families of wreath products of Abelian groups with symmetric groups realise families of subset triples with a simultaneous version of the TPP, then there are matrix multiplication algorithms with essentially quadratic complexity. Most researchers believe that this is indeed the case.[15] However, Alon, Shpilka and Chris Umans have recently shown that some of these conjectures implying fast matrix multiplication are incompatible with another plausible conjecture, the sunflower conjecture.[16]
Freivalds' algorithm is a simple Monte Carlo algorithm that given matrices A, B, C verifies in Θ(n2) time if AB = C.
Block matrix multiplication. In the 2D algorithm, each processor is responsible for one submatrix of C. In the 3D algorithm, every pair of submatrices from A and B that is multiplied is assigned to one processor.
Parallel matrix multiplication
Because of the nature of matrix operations and the layout of matrices in memory, it is typically possible to gain substantial performance gains through use of parallelization and vectorization. Several algorithms are possible, among which divide and conquer algorithms based on the block matrix decompositionIt should be noted that some lower time-complexity algorithms on paper may have indirect time complexity costs on real machines.
Communication-avoiding and distributed algorithms
On modern architectures with hierarchical memory, the cost of loading and storing input matrix elements tends to dominate the cost of arithmetic. On a single machine this is the amount of data transferred between RAM and cache, while on a distributed memory multi-node machine it is the amount transferred between nodes; in either case it is called the communication bandwidth. The naïve algorithm using three nested loops uses Ω(n3) communication bandwidth.Cannon's algorithm, also known as the 2D algorithm, partitions each input matrix into a block matrix whose elements are submatrices of size √M/3 by √M/3, where M is the size of fast memory.[18] The naïve algorithm is then used over the block matrices, computing products of submatrices entirely in fast memory. This reduces communication bandwidth to O(n3/√M), which is asymptotically optimal (for algorithms performing Ω(n3) computation).[19][20]
In a distributed setting with p processors arranged in a √p by √p 2D mesh, one submatrix of the result can be assigned to each processor, and the product can be computed with each processor transmitting O(n2/√p) words, which is asymptotically optimal assuming that each node stores the minimum O(n2/p) elements.[20] This can be improved by the 3D algorithm, which arranges the processors in a 3D cube mesh, assigning every product of two input submatrices to a single processor. The result submatrices are then generated by performing a reduction over each row.[21] This algorithm transmits O(n2/p2/3) words per processor, which is asymptotically optimal.[20] However, this requires replicating each input matrix element p1/3 times, and so requires a factor of p1/3 more memory than is needed to store the inputs. This algorithm can be combined with Strassen to further reduce runtime.[21] "2.5D" algorithms provide a continuous tradeoff between memory usage and communication bandwidth.[22] On modern distributed computing environments such as MapReduce, specialized multiplication algorithms have been developed.[23]
Other forms of multiplication
Some other ways to multiply two matrices are given below; some, in fact, are simpler than the definition above. The Cracovian product is yet another form.Hadamard product
Main article: Hadamard product (matrices)
For two matrices of the same dimensions, there is the Hadamard product, also known as the element-wise product, pointwise product, entrywise product and the Schur product.[24] For two matrices A and B of the same dimensions, the Hadamard product A ○ B is a matrix of the same dimensions, the i, j element of A is multiplied with the i, j element of B, that is:Frobenius product
The Frobenius inner product, sometimes denoted A : B, is the component-wise inner product of two matrices as though they are vectors. It is also the sum of the entries of the Hadamard product. Explicitly,Kronecker product
Main article: Kronecker product
For two matrices A and B of any different dimensions m × n and p × q respectively (no constraints on the dimensions of each matrix), the Kronecker product is the matrix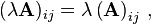






















![\begin{align}
\mathbf{ABC} & = \begin{pmatrix}
a & b & c
\end{pmatrix} \left[\begin{pmatrix}
\alpha & \beta & \gamma \\
\lambda & \mu & \nu \\
\rho & \sigma & \tau \\
\end{pmatrix} \begin{pmatrix}
x \\
y \\
z
\end{pmatrix} \right] = \left[ \begin{pmatrix}
a & b & c
\end{pmatrix} \begin{pmatrix}
\alpha & \beta & \gamma \\
\lambda & \mu & \nu \\
\rho & \sigma & \tau \\
\end{pmatrix} \right] \begin{pmatrix}
x \\
y \\
z
\end{pmatrix} \\
& = \begin{pmatrix}
a & b & c
\end{pmatrix}\begin{pmatrix}
\alpha x + \beta y + \gamma z \\
\lambda x + \mu y + \nu z \\
\rho x + \sigma y + \tau z \\
\end{pmatrix} = \begin{pmatrix}
a\alpha + b\lambda + c\rho & a\beta + b\mu + c\sigma & a\gamma + b\nu + c\tau
\end{pmatrix} \begin{pmatrix}
x \\
y \\
z
\end{pmatrix}\\
& = a\alpha x + b\lambda x + c\rho x + a\beta y + b\mu y + c\sigma y + a\gamma z + b\nu z + c\tau z \,,\end{align}](https://upload.wikimedia.org/math/3/c/d/3cd7e0377ca06fe721101c51a0d9b084.png)



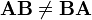

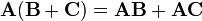
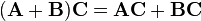

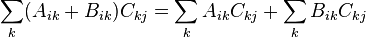
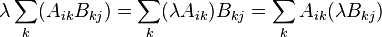
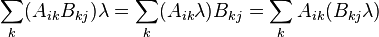
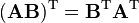
![\begin{align}
\left[(\mathbf{AB})^\mathrm{T}\right]_{ij}&=\left(\mathbf{AB}\right)_{ji}\\
&=\sum_k\left(\mathbf{A}\right)_{jk}\left(\mathbf{B}\right)_{ki}\\
&=\sum_k\left(\mathbf{A}^\mathrm{T}\right)_{kj}\left(\mathbf{B}^\mathrm{T}\right)_{ik}\\
&=\sum_k\left(\mathbf{B}^\mathrm{T}\right)_{ik}\left(\mathbf{A}^\mathrm{T}\right)_{kj}\\
&=\left[\left(\mathbf{B}^\mathrm{T}\right)\left(\mathbf{A}^\mathrm{T}\right)\right]_{ij}
\end{align}](https://upload.wikimedia.org/math/e/7/d/e7d94f9d16d1e7e1ab6ff24e34c233ea.png)
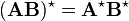
![\begin{align}
\left[(\mathbf{AB})^\star\right]_{ij}&=\left[\sum_k\left(\mathbf{A}\right)_{ik}\left(\mathbf{B}\right)_{kj}\right]^\star\\
&=\sum_k\left(\mathbf{A}\right)^\star_{ik}\left(\mathbf{B}\right)^\star_{kj}\\
&=\sum_k\left(\mathbf{A}^\star\right)_{ik}\left(\mathbf{B}^\star\right)_{kj}\\
&=\left(\mathbf{A}^\star\mathbf{B}^\star\right)_{ij}
\end{align}](https://upload.wikimedia.org/math/2/3/e/23e072cf0ded92d8de3da3c256e523dd.png)

![\begin{align}
\left[(\mathbf{AB})^\dagger\right]_{ij} &=\left[\left(\mathbf{AB}\right)^\star\right]_{ji}\\
&=\sum_k\left(\mathbf{A}^\star\right)_{jk}\left(\mathbf{B}^\star\right)_{ki}\\
&=\sum_k\left(\mathbf{A}^\dagger\right)_{kj}\left(\mathbf{B}^\dagger\right)_{ik}\\
&=\sum_k\left(\mathbf{B}^\dagger\right)_{ik}\left(\mathbf{A}^\dagger\right)_{kj}\\
&=\left[\left(\mathbf{B}^\dagger\right)\left(\mathbf{A}^\dagger\right)\right]_{ij}
\end{align}](https://upload.wikimedia.org/math/b/e/e/bee24d07fb1d862f91f273c940b08dd4.png)




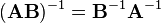

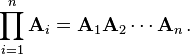
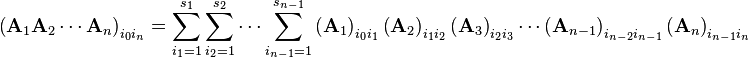

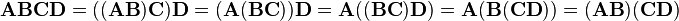
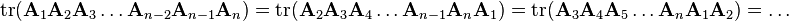
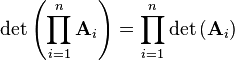

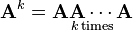
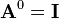
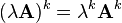





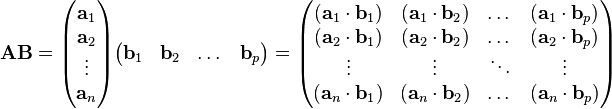









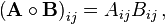

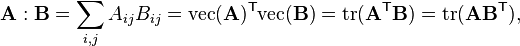
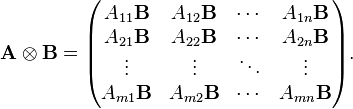
No comments:
Post a Comment