Sunday, 1 November 2015

3-sphere

3-sphere

From Wikipedia, the free encyclopedia
Stereographic projection of the hypersphere's parallels (red), meridians (blue) and hypermeridians (green). Because this projection is conformal, the curves intersect each other orthogonally (in the yellow points) as in 4D. All curves are circles: the curves that intersect <0,0,0,1> have infinite radius (= straight line).
In mathematics, a 3-sphere (also called a glome) is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space. Just as an ordinary sphere (or 2-sphere) is a two-dimensional surface that forms the boundary of a ball in three dimensions, a 3-sphere is an object with three dimensions that forms the boundary of a ball in four dimensions. A 3-sphere is an example of a 3-manifold.

Contents

Definition

In coordinates, a 3-sphere with center (C0, C1, C2, C3) and radius r is the set of all points (x0, x1, x2, x3) in real, 4-dimensional space (R4) such that
\sum_{i=0}^3(x_i - C_i)^2 = ( x_0 - C_0 )^2 + ( x_1 - C_1 )^2 + ( x_2 - C_2 )^2+ ( x_3 - C_3 )^2 = r^2.
The 3-sphere centered at the origin with radius 1 is called the unit 3-sphere and is usually denoted S3:
S^3 = \left\{(x_0,x_1,x_2,x_3)\in\mathbb{R}^4 : x_0^2 + x_1^2 + x_2^2 + x_3^2 = 1\right\}.
It is often convenient to regard R4 as the space with 2 complex dimensions (C2) or the quaternions (H). The unit 3-sphere is then given by
S^3 = \left\{(z_1,z_2)\in\mathbb{C}^2 : |z_1|^2 + |z_2|^2 = 1\right\}
or
S^3 = \left\{q\in\mathbb{H} : ||q|| = 1\right\}.
This description as the quaternions of norm one, identifies the 3-sphere with the versors in the quaternion division ring. Just as the unit circle is important for planar polar coordinates, so the 3-sphere is important in the polar view of 4-space involved in quaternion multiplication. See polar decomposition of a quaternion for details of this development of the three-sphere. This view of the 3-sphere is the basis for the study of elliptic space as developed by Georges Lemaître[1]

Properties

Elementary properties

The 3-dimensional cubic hyperarea of a 3-sphere of radius r is
2\pi^2 r^3 \,
while the 4-dimensional quartic hypervolume (the volume of the 4-dimensional region bounded by the 3-sphere) is
\begin{matrix} \frac{1}{2} \end{matrix} \pi^2 r^4.
Every non-empty intersection of a 3-sphere with a three-dimensional hyperplane is a 2-sphere (unless the hyperplane is tangent to the 3-sphere, in which case the intersection is a single point). As a 3-sphere moves through a given three-dimensional hyperplane, the intersection starts out as a point, then becomes a growing 2-sphere that reaches its maximal size when the hyperplane cuts right through the "equator" of the 3-sphere. Then the 2-sphere shrinks again down to a single point as the 3-sphere leaves the hyperplane.

Topological properties

A 3-sphere is a compact, connected, 3-dimensional manifold without boundary. It is also simply connected. What this means, in the broad sense, is that any loop, or circular path, on the 3-sphere can be continuously shrunk to a point without leaving the 3-sphere. The Poincaré conjecture, proved in 2003 by Grigori Perelman, provides that the 3-sphere is the only three-dimensional manifold (up to homeomorphism) with these properties.
The 3-sphere is homeomorphic to the one-point compactification of \mathbb{R}^3. In general, any topological space that is homeomorphic to the 3-sphere is called a topological 3-sphere.
The homology groups of the 3-sphere are as follows: H0(S3,Z) and H3(S3,Z) are both infinite cyclic, while Hi(S3,Z) = {0} for all other indices i. Any topological space with these homology groups is known as a homology 3-sphere. Initially Poincaré conjectured that all homology 3-spheres are homeomorphic to S3, but then he himself constructed a non-homeomorphic one, now known as the Poincaré homology sphere. Infinitely many homology spheres are now known to exist. For example, a Dehn filling with slope 1/n on any knot in the three-sphere gives a homology sphere; typically these are not homeomorphic to the three-sphere.
As to the homotopy groups, we have π1(S3) = π2(S3) = {0} and π3(S3) is infinite cyclic. The higher-homotopy groups (k ≥ 4) are all finite abelian but otherwise follow no discernible pattern. For more discussion see homotopy groups of spheres.
Homotopy groups of S3
k 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
πk(S3) 0 0 0 Z Z2 Z2 Z12 Z2 Z2 Z3 Z15 Z2 Z2⊕Z2 Z12⊕Z2 Z84⊕Z2⊕Z2 Z2⊕Z2 Z6

Geometric properties

The 3-sphere is naturally a smooth manifold, in fact, a closed embedded submanifold of R4. The Euclidean metric on R4 induces a metric on the 3-sphere giving it the structure of a Riemannian manifold. As with all spheres, the 3-sphere has constant positive sectional curvature equal to 1/r2 where r is the radius.
Much of the interesting geometry of the 3-sphere stems from the fact that the 3-sphere has a natural Lie group structure given by quaternion multiplication (see the section below on group structure). The only other spheres with such a structure are the 0-sphere and the 1-sphere (see circle group).
Unlike the 2-sphere, the 3-sphere admits nonvanishing vector fields (sections of its tangent bundle). One can even find three linearly independent and nonvanishing vector fields. These may be taken to be any left-invariant vector fields forming a basis for the Lie algebra of the 3-sphere. This implies that the 3-sphere is parallelizable. It follows that the tangent bundle of the 3-sphere is trivial. For a general discussion of the number of linear independent vector fields on a n-sphere, see the article vector fields on spheres.
There is an interesting action of the circle group T on S3 giving the 3-sphere the structure of a principal circle bundle known as the Hopf bundle. If one thinks of S3 as a subset of C2, the action is given by
(z_1,z_2)\cdot\lambda = (z_1\lambda,z_2\lambda)\quad \forall\lambda\in\mathbb T.
The orbit space of this action is homeomorphic to the two-sphere S2. Since S3 is not homeomorphic to S2×S1, the Hopf bundle is nontrivial.

Topological construction

There are several well-known constructions of the three-sphere. Here we describe gluing a pair of three-balls and then the one-point compactification.

Gluing

A 3-sphere can be constructed topologically by "gluing" together the boundaries of a pair of 3-balls. The boundary of a 3-ball is a 2-sphere, and these two 2-spheres are to be identified. That is, imagine a pair of 3-balls of the same size, then superpose them so that their 2-spherical boundaries match, and let matching pairs of points on the pair of 2-spheres be identically equivalent to each other. In analogy with the case of the 2-sphere (see below), the gluing surface is called an equatorial sphere.
Note that the interiors of the 3-balls are not glued to each other. One way to think of the fourth dimension is as a continuous real-valued function of the 3-dimensional coordinates of the 3-ball, perhaps considered to be "temperature". We take the "temperature" to be zero along the gluing 2-sphere and let one of the 3-balls be "hot" and let the other 3-ball be "cold". The "hot" 3-ball could be thought of as the "upper hemisphere" and the "cold" 3-ball could be thought of as the "lower hemisphere". The temperature is highest/lowest at the centers of the two 3-balls.
This construction is analogous to a construction of a 2-sphere, performed by gluing the boundaries of a pair of disks. A disk is a 2-ball, and the boundary of a disk is a circle (a 1-sphere). Let a pair of disks be of the same diameter. Superpose them and glue corresponding points on their boundaries. Again one may think of the third dimension as temperature. Likewise, we may inflate the 2-sphere, moving the pair of disks to become the northern and southern hemispheres.

One-point compactification

After removing a single point from the 2-sphere, what remains is homeomorphic to the Euclidean plane. In the same way, removing a single point from the 3-sphere yields three-dimensional space. An extremely useful way to see this is via stereographic projection. We first describe the lower-dimensional version.
Rest the south pole of a unit 2-sphere on the xy-plane in three-space. We map a point p of the sphere (minus the north pole N) to the plane by sending p to the intersection of the line Np with the plane. Stereographic projection of a 3-sphere (again removing the north pole) maps to three-space in the same manner. (Notice that, since stereographic projection is conformal, round spheres are sent to round spheres or to planes.)
A somewhat different way to think of the one-point compactification is via the exponential map. Returning to our picture of the unit two-sphere sitting on the Euclidean plane: Consider a geodesic in the plane, based at the origin, and map this to a geodesic in the two-sphere of the same length, based at the south pole. Under this map all points of the circle of radius \pi are sent to the north pole. Since the open unit disk is homeomorphic to the Euclidean plane, this is again a one-point compactification.
The exponential map for 3-sphere is similarly constructed; it may also be discussed using the fact that the 3-sphere is the Lie group of unit quaternions.

Coordinate systems on the 3-sphere

The four Euclidean coordinates for S3 are redundant since they are subject to the condition that {x_0}^2 + {x_1}^2 + {x_2}^2 + {x_3}^2 = 1. As a 3-dimensional manifold one should be able to parameterize S3 by three coordinates, just as one can parameterize the 2-sphere using two coordinates (such as latitude and longitude). Due to the nontrivial topology of S3 it is impossible to find a single set of coordinates that cover the entire space. Just as on the 2-sphere, one must use at least two coordinate charts. Some different choices of coordinates are given below.

Hyperspherical coordinates

It is convenient to have some sort of hyperspherical coordinates on S3 in analogy to the usual spherical coordinates on S2. One such choice — by no means unique — is to use (ψ, θ, φ), where
x_0 = r\cos\psi\
x_1 = r\sin\psi \cos\theta\
x_2 = r\sin\psi \sin\theta \cos\phi\
x_3 = r\sin\psi \sin\theta \sin\phi\
where ψ and θ run over the range 0 to π, and φ runs over 0 to 2π. Note that, for any fixed value of ψ, θ and φ parameterize a 2-sphere of radius sin(ψ), except for the degenerate cases, when ψ equals 0 or π, in which case they describe a point.
The round metric on the 3-sphere in these coordinates is given by
ds^2 = r^2 \left[ d\psi^2 + \sin^2\psi\left(d\theta^2 + \sin^2\theta\, d\phi^2\right) \right]
and the volume form by
dV =r^3 \left(\sin^2\psi\,\sin\theta\right)\,dr\wedge d\psi\wedge d\theta\wedge d\phi.
These coordinates have an elegant description in terms of quaternions. Any unit quaternion q can be written as a versor:
q = eτψ = cos ψ + τ sin ψ
where τ is a unit imaginary quaternion; that is, a quaternion that satisfies τ2 = −1. This is the quaternionic analogue of Euler's formula. Now the unit imaginary quaternions all lie on the unit 2-sphere in Im H so any such τ can be written:
τ = cos θ i + sin θ cos φ j + sin θ sin φ k
With τ in this form, the unit quaternion q is given by
q = eτψ = x0 + x1 i + x2 j + x3 k
where the x’s are as above.
When q is used to describe spatial rotations (cf. quaternions and spatial rotations), it describes a rotation about τ through an angle of 2ψ.

Hopf coordinates

The Hopf fibration can be visualized using a stereographic projection of S3 to R3 and then compressing R3 to a ball. This image shows points on S2 and their corresponding fibers with the same color.
For unit radius another choice of hyperspherical coordinates, (η, ξ1, ξ2), makes use of the embedding of S3 in C2. In complex coordinates (z1, z2) ∈ C2 we write
z_1 = e^{i\,\xi_1}\sin\eta
z_2 = e^{i\,\xi_2}\cos\eta.
This could also be expressed in R4 as
x_0 = \cos\xi_1\sin\eta
x_1 = \sin\xi_1\sin\eta
x_2 = \cos\xi_2\cos\eta
x_3 = \sin\xi_2\cos\eta
Here η runs over the range 0 to π/2, and ξ1 and ξ2 can take any values between 0 and 2π. These coordinates are useful in the description of the 3-sphere as the Hopf bundle
S^1 \to S^3 \to S^2.\,
A diagram depicting the poloidal (ξ1) direction, represented by the red arrow, and the toroidal (ξ2) direction, represented by the blue arrow, although the terms poloidal and toroidal are arbitrary in this flat torus case.
For any fixed value of η between 0 and π/2, the coordinates (ξ1, ξ2) parameterize a 2-dimensional torus. Rings of constant ξ1 and ξ2 above form simple orthogonal grids on the tori. See image to right. In the degenerate cases, when η equals 0 or π/2, these coordinates describe a circle.
The round metric on the 3-sphere in these coordinates is given by
ds^2 = d\eta^2 + \sin^2\eta\,d\xi_1^2 + \cos^2\eta\,d\xi_2^2
and the volume form by
dV = \sin\eta\cos\eta\,d\eta\wedge d\xi_1\wedge d\xi_2.
To get the interlocking circles of the Hopf fibration, make a simple substitution in the equations above[2]
z_1 = e^{i\,(\xi_1+\xi_2)}\sin\eta
z_2 = e^{i\,(\xi_1-\xi_2)}\cos\eta.
In this case η, ξ1 specify which circle, and ξ2 specifies the position along each circle. One round trip (0 to 2π) of either ξ1 or ξ2 causes you to make one full circle of both limbs of the torus.

Stereographic coordinates

Another convenient set of coordinates can be obtained via stereographic projection of S3 from a pole onto the corresponding equatorial R3 hyperplane. For example, if we project from the point (−1, 0, 0, 0) we can write a point p in S3 as
p = \left(\frac{1-\|u\|^2}{1+\|u\|^2}, \frac{2\mathbf{u}}{1+\|u\|^2}\right) = \frac{1+\mathbf{u}}{1-\mathbf{u}}
where u = (u1, u2, u3) is a vector in R3 and ||u||2 = u12 + u22 + u32. In the second equality above, we have identified p with a unit quaternion and u = u1 i + u2 j + u3 k with a pure quaternion. (Note that the numerator and denominator commute here even though quaternionic multiplication is generally noncommutative). The inverse of this map takes p = (x0, x1, x2, x3) in S3 to
\mathbf{u} = \frac{1}{1+x_0}\left(x_1, x_2, x_3\right).
We could just as well have projected from the point (1, 0, 0, 0), in which case the point p is given by
p = \left(\frac{-1+\|v\|^2}{1+\|v\|^2}, \frac{2\mathbf{v}}{1+\|v\|^2}\right) = \frac{-1+\mathbf{v}}{1+\mathbf{v}}
where v = (v1, v2, v3) is another vector in R3. The inverse of this map takes p to
\mathbf{v} = \frac{1}{1-x_0}\left(x_1,x_2,x_3\right).
Note that the u coordinates are defined everywhere but (−1, 0, 0, 0) and the v coordinates everywhere but (1, 0, 0, 0). This defines an atlas on S3 consisting of two coordinate charts or "patches", which together cover all of S3. Note that the transition function between these two charts on their overlap is given by
\mathbf{v} = \frac{1}{\|u\|^2}\mathbf{u}
and vice versa.

Group structure

When considered as the set of unit quaternions, S3 inherits an important structure, namely that of quaternionic multiplication. Because the set of unit quaternions is closed under multiplication, S3 takes on the structure of a group. Moreover, since quaternionic multiplication is smooth, S3 can be regarded as a real Lie group. It is a nonabelian, compact Lie group of dimension 3. When thought of as a Lie group S3 is often denoted Sp(1) or U(1, H).
It turns out that the only spheres that admit a Lie group structure are S1, thought of as the set of unit complex numbers, and S3, the set of unit quaternions. One might think that S7, the set of unit octonions, would form a Lie group, but this fails since octonion multiplication is nonassociative. The octonionic structure does give S7 one important property: parallelizability. It turns out that the only spheres that are parallelizable are S1, S3, and S7.
By using a matrix representation of the quaternions, H, one obtains a matrix representation of S3. One convenient choice is given by the Pauli matrices:
x_1+ x_2 i + x_3 j + x_4 k \mapsto \begin{pmatrix}\;\;\,x_1 + i x_2 & x_3 + i x_4 \\ -x_3 + i x_4 & x_1 - i x_2\end{pmatrix}.
This map gives an injective algebra homomorphism from H to the set of 2×2 complex matrices. It has the property that the absolute value of a quaternion q is equal to the square root of the determinant of the matrix image of q.
The set of unit quaternions is then given by matrices of the above form with unit determinant. This matrix subgroup is precisely the special unitary group SU(2). Thus, S3 as a Lie group is isomorphic to SU(2).
Using our Hopf coordinates (η, ξ1, ξ2) we can then write any element of SU(2) in the form
\begin{pmatrix}e^{i\,\xi_1}\sin\eta & e^{i\,\xi_2}\cos\eta \\ -e^{-i\,\xi_2}\cos\eta & e^{-i\,\xi_1}\sin\eta\end{pmatrix}.
Another way to state this result is if we express the matrix representation of an element of SU(2) as a linear combination of the Pauli matrices. It is seen that an arbitrary element U \in SU(2) can be written as U=\alpha_0 I + \sum_{i=1}^3\alpha_i J_i. The condition that the determinant of U is +1 implies that the coefficients 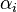\alpha_i are constrained to lie on a 3-sphere.

In literature

In Edwin Abbott Abbott's Flatland, published in 1884, and in Sphereland, a 1965 sequel to Flatland by Dionys Burger, the 3-sphere is referred to as an oversphere, and a 4-sphere is referred to as a hypersphere.
Writing in the American Journal of Physics,[3] Mark A. Peterson describes three different ways of visualizing 3-spheres and points out language in The Divine Comedy that suggests Dante viewed the Universe in the same way.

See also

References


  • Georges Lemaître (1948) "Quaternions et espace elliptique", Acta Pontifical Academy of Sciences 12:57–78

  • Banchoff, Thomas. "The Flat Torus in the Three-Sphere".

    1. Mark A. Peterson. "Dante and the 3-sphere", American Journal of Physics, vol 47, number 12, 1979, pp1031-1035
    • David W. Henderson, Experiencing Geometry: In Euclidean, Spherical, and Hyperbolic Spaces, second edition, 2001, [1] (Chapter 20: 3-spheres and hyperbolic 3-spaces.)
    • Jeffrey R. Weeks, The Shape of Space: How to Visualize Surfaces and Three-dimensional Manifolds, 1985, ([2]) (Chapter 14: The Hypersphere) (Says: A Warning on terminology: Our two-sphere is defined in three-dimensional space, where it is the boundary of a three-dimensional ball. This terminology is standard among mathematicians, but not among physicists. So don't be surprised if you find people calling the two-sphere a three-sphere.)

    External links

    Posted by at

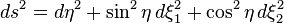
    No comments:

    Post a Comment

    Subscribe to: Post Comments (Atom)