Sunday, 1 November 2015

Knot theory

Knot theory

From Wikipedia, the free encyclopedia
A three-dimensional depiction of a thickened trefoil knot, the simplest non-trivial knot
A knot diagram of the trefoil knot
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3 (in topology, a circle isn't bound to the classical geometric concept, but to all of its homeomorphisms). Two mathematical knots are equivalent if one can be transformed into the other via a deformation of R3 upon itself (known as an ambient isotopy); these transformations correspond to manipulations of a knotted string that do not involve cutting the string or passing the string through itself.
Knots can be described in various ways. Given a method of description, however, there may be more than one description that represents the same knot. For example, a common method of describing a knot is a planar diagram called a knot diagram. Any given knot can be drawn in many different ways using a knot diagram. Therefore, a fundamental problem in knot theory is determining when two descriptions represent the same knot.
A complete algorithmic solution to this problem exists, which has unknown complexity. In practice, knots are often distinguished by using a knot invariant, a "quantity" which is the same when computed from different descriptions of a knot. Important invariants include knot polynomials, knot groups, and hyperbolic invariants.
The original motivation for the founders of knot theory was to create a table of knots and links, which are knots of several components entangled with each other. Over six billion knots and links have been tabulated since the beginnings of knot theory in the 19th century.
To gain further insight, mathematicians have generalized the knot concept in several ways. Knots can be considered in other three-dimensional spaces and objects other than circles can be used; see knot (mathematics). Higher-dimensional knots are n-dimensional spheres in m-dimensional Euclidean space.

Contents

History

Main article: History of knot theory
Intricate Celtic knotwork in the 1200-year-old Book of Kells
Archaeologists have discovered that knot tying dates back to prehistoric times. Besides their uses such as recording information and tying objects together, knots have interested humans for their aesthetics and spiritual symbolism. Knots appear in various forms of Chinese artwork dating from several centuries BC (see Chinese knotting). The endless knot appears in Tibetan Buddhism, while the Borromean rings have made repeated appearances in different cultures, often representing strength in unity. The Celtic monks who created the Book of Kells lavished entire pages with intricate Celtic knotwork.
A mathematical theory of knots was first developed in 1771 by Alexandre-Théophile Vandermonde who explicitly noted the importance of topological features when discussing the properties of knots related to the geometry of position. Mathematical studies of knots began in the 19th century with Gauss, who defined the linking integral (Silver 2006). In the 1860s, Lord Kelvin's theory that atoms were knots in the aether led to Peter Guthrie Tait's creation of the first knot tables for complete classification. Tait, in 1885, published a table of knots with up to ten crossings, and what came to be known as the Tait conjectures. This record motivated the early knot theorists, but knot theory eventually became part of the emerging subject of topology.
The first knot tabulator, Peter Guthrie Tait
These topologists in the early part of the 20th century—Max Dehn, J. W. Alexander, and others—studied knots from the point of view of the knot group and invariants from homology theory such as the Alexander polynomial. This would be the main approach to knot theory until a series of breakthroughs transformed the subject.
In the late 1970s, William Thurston introduced hyperbolic geometry into the study of knots with the hyperbolization theorem. Many knots were shown to be hyperbolic knots, enabling the use of geometry in defining new, powerful knot invariants. The discovery of the Jones polynomial by Vaughan Jones in 1984 (Sossinsky 2002, pp. 71–89), and subsequent contributions from Edward Witten, Maxim Kontsevich, and others, revealed deep connections between knot theory and mathematical methods in statistical mechanics and quantum field theory. A plethora of knot invariants have been invented since then, utilizing sophisticated tools such as quantum groups and Floer homology.
In the last several decades of the 20th century, scientists became interested in studying physical knots in order to understand knotting phenomena in DNA and other polymers. Knot theory can be used to determine if a molecule is chiral (has a "handedness") or not (Simon 1986). Tangles, strings with both ends fixed in place, have been effectively used in studying the action of topoisomerase on DNA (Flapan 2000). Knot theory may be crucial in the construction of quantum computers, through the model of topological quantum computation (Collins 2006).

Knot equivalence

On the left, the unknot, and a knot equivalent to it. It can be more difficult to determine whether complex knots, such as the one on the right, are equivalent to the unknot.
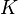A knot is created by beginning with a one-dimensional line segment, wrapping it around itself arbitrarily, and then fusing its two free ends together to form a closed loop (Adams 2004) (Sossinsky 2002). Simply, we can say a knot K is an injective and continuous function K:[0,1]\to \mathbb{R}^3 with K(0)=K(1). When topologists consider knots and other entanglements such as links and braids, they consider the space surrounding the knot as a viscous fluid. If the knot can be pushed about smoothly in the fluid, without intersecting itself, to coincide with another knot, the two knots are considered equivalent. The idea of knot equivalence is to give a precise definition of when two knots should be considered the same even when positioned quite differently in space. A formal mathematical definition is that two knots K_1,K_2 are equivalent if there is an orientation-preserving homeomorphism h\colon\R^3\to\R^3 with h(K_1)=K_2, and this is known as an ambient isotopy.
The basic problem of knot theory, the recognition problem, is determining the equivalence of two knots. Algorithms exist to solve this problem, with the first given by Wolfgang Haken in the late 1960s (Hass 1998). Nonetheless, these algorithms can be extremely time-consuming, and a major issue in the theory is to understand how hard this problem really is (Hass 1998). The special case of recognizing the unknot, called the unknotting problem, is of particular interest (Hoste 2005).

Knot diagrams

A useful way to visualise and manipulate knots is to project the knot onto a plane—think of the knot casting a shadow on the wall. A small change in the direction of projection will ensure that it is one-to-one except at the double points, called crossings, where the "shadow" of the knot crosses itself once transversely (Rolfsen 1976). At each crossing, to be able to recreate the original knot, the over-strand must be distinguished from the under-strand. This is often done by creating a break in the strand going underneath. The resulting diagram is an immersed plane curve with the additional data of which strand is over and which is under at each crossing. (These diagrams are called knot diagrams when they represent a knot and link diagrams when they represent a link.) Analogously, knotted surfaces in 4-space can be related to immersed surfaces in 3-space.
A reduced diagram is a knot diagram in which there are no reducible crossings (also nugatory or removable crossings), or in which all of the reducible crossings have been removed.(Weisstein, ReducedKnotDiagram)(Weisstein, ReducibleCrossing)

Reidemeister moves

Main article: Reidemeister move
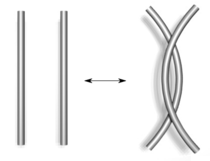
In 1927, working with this diagrammatic form of knots, J. W. Alexander and G. B. Briggs, and independently Kurt Reidemeister, demonstrated that two knot diagrams belonging to the same knot can be related by a sequence of three kinds of moves on the diagram, shown below. These operations, now called the Reidemeister moves, are:
  1. Twist and untwist in either direction.
  2. Move one strand completely over another.
  3. Move a strand completely over or under a crossing.
Reidemeister moves
Reidemeister move 1.png Frame left.png Reidemeister move 2.png
Type I Type II
Reidemeister move 3.png
Type III
The proof that diagrams of equivalent knots are connected by Reidemeister moves relies on an analysis of what happens under the planar projection of the movement taking one knot to another. The movement can be arranged so that almost all of the time the projection will be a knot diagram, except at finitely many times when an "event" or "catastrophe" occurs, such as when more than two strands cross at a point or multiple strands become tangent at a point. A close inspection will show that complicated events can be eliminated, leaving only the simplest events: (1) a "kink" forming or being straightened out; (2) two strands becoming tangent at a point and passing through; and (3) three strands crossing at a point. These are precisely the Reidemeister moves (Sossinsky 2002, ch. 3) (Lickorish 1997, ch. 1).

Knot invariants

Main article: Knot invariant
A knot invariant is a "quantity" that is the same for equivalent knots (Adams 2004)(Lickorish 1997)(Rolfsen 1976). For example, if the invariant is computed from a knot diagram, it should give the same value for two knot diagrams representing equivalent knots. An invariant may take the same value on two different knots, so by itself may be incapable of distinguishing all knots. An elementary invariant is tricolorability.
"Classical" knot invariants include the knot group, which is the fundamental group of the knot complement, and the Alexander polynomial, which can be computed from the Alexander invariant, a module constructed from the infinite cyclic cover of the knot complement (Lickorish 1997)(Rolfsen 1976). In the late 20th century, invariants such as "quantum" knot polynomials, Vassiliev invariants and hyperbolic invariants were discovered. These aforementioned invariants are only the tip of the iceberg of modern knot theory.

Knot polynomials

Main article: Knot polynomial
A knot polynomial is a knot invariant that is a polynomial. Well-known examples include the Jones and Alexander polynomials. A variant of the Alexander polynomial, the Alexander–Conway polynomial, is a polynomial in the variable z with integer coefficients (Lickorish 1997).
The Alexander–Conway polynomial is actually defined in terms of links, which consist of one or more knots entangled with each other. The concepts explained above for knots, e.g. diagrams and Reidemeister moves, also hold for links.
Consider an oriented link diagram, i.e. one in which every component of the link has a preferred direction indicated by an arrow. For a given crossing of the diagram, let L_+, L_-, L_0 be the oriented link diagrams resulting from changing the diagram as indicated in the figure:
Skein (HOMFLY).svg
The original diagram might be either L_+ or L_-, depending on the chosen crossing's configuration. Then the Alexander–Conway polynomial, C(z), is recursively defined according to the rules:
  • C(O) = 1 (where O is any diagram of the unknot)
  • C(L_+) = C(L_-) + z C(L_0).
The second rule is what is often referred to as a skein relation. To check that these rules give an invariant of an oriented link, one should determine that the polynomial does not change under the three Reidemeister moves. Many important knot polynomials can be defined in this way.
The following is an example of a typical computation using a skein relation. It computes the Alexander–Conway polynomial of the trefoil knot. The yellow patches indicate where the relation is applied.
C(Skein-relation-trefoil-plus-sm.png) = C(Skein-relation-trefoil-minus-sm.png) + z C(Skein-relation-trefoil-zero-sm.png)
gives the unknot and the Hopf link. Applying the relation to the Hopf link where indicated,
C(Skein-relation-link22-plus-sm.png) = C(Skein-relation-link22-minus-sm.png) + z C(Skein-relation-link22-zero-sm.png)
gives a link deformable to one with 0 crossings (it is actually the unlink of two components) and an unknot. The unlink takes a bit of sneakiness:
C(Skein-relation-link20-plus-sm.png) = C(Skein-relation-link20-minus-sm.png) + z C(Skein-relation-link20-zero-sm.png)
which implies that C(unlink of two components) = 0, since the first two polynomials are of the unknot and thus equal.
Putting all this together will show:
C(trefoil) = 1 + z(0 + z) = 1 + z2.
Since the Alexander–Conway polynomial is a knot invariant, this shows that the trefoil is not equivalent to the unknot. So the trefoil really is "knotted".
  • The left handed trefoil knot.
  • The right handed trefoil knot.
Actually, there are two trefoil knots, called the right and left-handed trefoils, which are mirror images of each other (take a diagram of the trefoil given above and change each crossing to the other way to get the mirror image). These are not equivalent to each other, meaning that they are not amphicheiral. This was shown by Max Dehn, before the invention of knot polynomials, using group theoretical methods (Dehn 1914). But the Alexander–Conway polynomial of each kind of trefoil will be the same, as can be seen by going through the computation above with the mirror image. The Jones polynomial can in fact distinguish between the left and right-handed trefoil knots (Lickorish 1997).

Hyperbolic invariants

William Thurston proved many knots are hyperbolic knots, meaning that the knot complement, i.e. the set of points of 3-space not on the knot, admits a geometric structure, in particular that of hyperbolic geometry. The hyperbolic structure depends only on the knot so any quantity computed from the hyperbolic structure is then a knot invariant (Adams 2004).
  • The Borromean rings are a link with the property that removing one ring unlinks the others.
  • SnapPea's cusp view: the Borromean rings complement from the perspective of an inhabitant living near the red component.
Geometry lets us visualize what the inside of a knot or link complement looks like by imagining light rays as traveling along the geodesics of the geometry. An example is provided by the picture of the complement of the Borromean rings. The inhabitant of this link complement is viewing the space from near the red component. The balls in the picture are views of horoball neighborhoods of the link. By thickening the link in a standard way, the horoball neighborhoods of the link components are obtained. Even though the boundary of a neighborhood is a torus, when viewed from inside the link complement, it looks like a sphere. Each link component shows up as infinitely many spheres (of one color) as there are infinitely many light rays from the observer to the link component. The fundamental parallelogram (which is indicated in the picture), tiles both vertically and horizontally and shows how to extend the pattern of spheres infinitely.
This pattern, the horoball pattern, is itself a useful invariant. Other hyperbolic invariants include the shape of the fundamental paralleogram, length of shortest geodesic, and volume. Modern knot and link tabulation efforts have utilized these invariants effectively. Fast computers and clever methods of obtaining these invariants make calculating these invariants, in practice, a simple task (Adams, Hildebrand & Weeks 1991).

Higher dimensions

A knot in three dimensions can be untied when placed in four-dimensional space. This is done by changing crossings. Suppose one strand is behind another as seen from a chosen point. Lift it into the fourth dimension, so there is no obstacle (the front strand having no component there); then slide it forward, and drop it back, now in front. Analogies for the plane would be lifting a string up off the surface, or removing a dot from inside a circle.
In fact, in four dimensions, any non-intersecting closed loop of one-dimensional string is equivalent to an unknot. First "push" the loop into a three-dimensional subspace, which is always possible, though technical to explain.

Knotting spheres of higher dimension

Since a knot can be considered topologically a 1-dimensional sphere, the next generalization is to consider a two-dimensional sphere embedded in a four-dimensional ball. Such an embedding is unknotted if there is a homeomorphism of the 4-sphere onto itself taking the 2-sphere to a standard "round" 2-sphere. Suspended knots and spun knots are two typical families of such 2-sphere knots.
The mathematical technique called "general position" implies that for a given n-sphere in the m-sphere, if m is large enough (depending on n), the sphere should be unknotted. In general, piecewise-linear n-spheres form knots only in (n + 2)-space (Zeeman 1963), although this is no longer a requirement for smoothly knotted spheres. In fact, there are smoothly knotted (4k − 1)-spheres in 6k-space, e.g. there is a smoothly knotted 3-sphere in the 6-sphere (Haefliger 1962)(Levine 1965). Thus the codimension of a smooth knot can be arbitrarily large when not fixing the dimension of the knotted sphere; however, any smooth k-sphere in an n-sphere with 2n − 3k − 3 > 0 is unknotted. The notion of a knot has further generalisations in mathematics, see: knot (mathematics), isotopy classification of embeddings.
Every knot in Sn is the link of a real-algebraic set with isolated singularity in Rn+1 (Akbulut & King 1981).
An n-knot is a single Sn embedded in Sm. An n-link is k-copies of Sn embedded in Sm, where k is a natural number. Both the m = n + 2 case and the m > n + 2 case are researched well. The n > 1 case has different futures from the n = 1 case and is an exciting field.[1] [2]

Adding knots

Main article: Knot sum
Adding two knots
Two knots can be added by cutting both knots and joining the pairs of ends. The operation is called the knot sum, or sometimes the connected sum or composition of two knots. This can be formally defined as follows (Adams 2004): consider a planar projection of each knot and suppose these projections are disjoint. Find a rectangle in the plane where one pair of opposite sides are arcs along each knot while the rest of the rectangle is disjoint from the knots. Form a new knot by deleting the first pair of opposite sides and adjoining the other pair of opposite sides. The resulting knot is a sum of the original knots. Depending on how this is done, two different knots (but no more) may result. This ambiguity in the sum can be eliminated regarding the knots as oriented, i.e. having a preferred direction of travel along the knot, and requiring the arcs of the knots in the sum are oriented consistently with the oriented boundary of the rectangle.
The knot sum of oriented knots is commutative and associative. A knot is prime if it is non-trivial and cannot be written as the knot sum of two non-trivial knots. A knot that can be written as such a sum is composite. There is a prime decomposition for knots, analogous to prime and composite numbers (Schubert 1949). For oriented knots, this decomposition is also unique. Higher-dimensional knots can also be added but there are some differences. While you cannot form the unknot in three dimensions by adding two non-trivial knots, you can in higher dimensions, at least when one considers smooth knots in codimension at least 3.

Tabulating knots

See also: List of prime knots and Knot tabulation
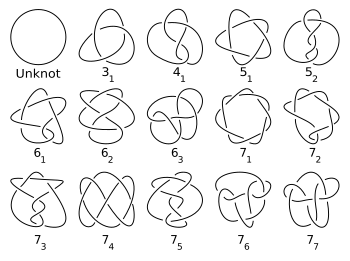
A table of prime knots up to seven crossings. The knots are labeled with Alexander–Briggs notation
Traditionally, knots have been catalogued in terms of crossing number. Knot tables generally include only prime knots, and only one entry for a knot and its mirror image (even if they are different) (Hoste, Thistlethwaite & Weeks 1998). The number of nontrivial knots of a given crossing number increases rapidly, making tabulation computationally difficult (Hoste 2005, p. 20). Tabulation efforts have succeeded in enumerating over 6 billion knots and links (Hoste 2005, p. 28). The sequence of the number of prime knots of a given crossing number, up to crossing number 16, is 0, 0, 1, 1, 2, 3, 7, 21, 49, 165, 552, 2176, 9988, 46972, 253293, 1388705... (sequence A002863 in OEIS). While exponential upper and lower bounds for this sequence are known, it has not been proven that this sequence is strictly increasing (Adams 2004).
The first knot tables by Tait, Little, and Kirkman used knot diagrams, although Tait also used a precursor to the Dowker notation. Different notations have been invented for knots which allow more efficient tabulation (Hoste 2005).
The early tables attempted to list all knots of at most 10 crossings, and all alternating knots of 11 crossings (Hoste, Thistlethwaite & Weeks 1998). The development of knot theory due to Alexander, Reidemeister, Seifert, and others eased the task of verification and tables of knots up to and including 9 crossings were published by Alexander–Briggs and Reidemeister in the late 1920s.
The first major verification of this work was done in the 1960s by John Horton Conway, who not only developed a new notation but also the Alexander–Conway polynomial (Conway 1970)(Doll & Hoste 1991). This verified the list of knots of at most 11 crossings and a new list of links up to 10 crossings. Conway found a number of omissions but only one duplication in the Tait–Little tables; however he missed the duplicates called the Perko pair, which would only be noticed in 1974 by Kenneth Perko (Perko 1974). This famous error would propagate when Dale Rolfsen added a knot table in his influential text, based on Conway's work. Conway's (only) paper on knot theory also contains a typographical duplication on its non-alternating 11-crossing knots page and omits 4 examples — 2 previously listed in D. Lombardero's 1968 Princeton senior thesis and 2 more subsequently discovered by A. Caudron. [see Perko (1982) Primality of certain knots, Topology Proceedings,] Less famous is the duplicate in his 10 crossing link table: 2.-2.-20.20 is the mirror of 8*-20:-20. [See Perko, A Short History of Non-cyclic Knot Theory, Conference on Knot Theory and its Applications to Physics and Quantum Computing, University of Texas at Dallas, January 2015.]
In the late 1990s Hoste, Thistlethwaite, and Weeks tabulated all the knots through 16 crossings (Hoste, Thistlethwaite & Weeks 1998). In 2003 Rankin, Flint, and Schermann, tabulated the alternating knots through 22 crossings (Hoste 2005).

Alexander–Briggs notation

This is the most traditional notation, due to the 1927 paper of J. W. Alexander and G. Briggs and later extended by Dale Rolfsen in his knot table (see image above and List of prime knots). The notation simply organizes knots by their crossing number. One writes the crossing number with a subscript to denote its order amongst all knots with that crossing number. This order is arbitrary and so has no special significance (though in each number of crossings the twist knot comes after the torus knot). Links are written by the crossing number with a superscript to denote the number of components and a subscript to denote its order within the links with the same number of components and crossings. Thus the trefoil knot is notated 31 and the Hopf link is 22
1.

Dowker notation

Main article: Dowker notation
A knot diagram with crossings labelled for a Dowker sequence
The Dowker notation, also called the Dowker–Thistlethwaite notation or code, for a knot is a finite sequence of even integers. The numbers are generated by following the knot and marking the crossings with consecutive integers. Since each crossing is visited twice, this creates a pairing of even integers with odd integers. An appropriate sign is given to indicate over and undercrossing. For example, in this figure the knot diagram has crossings labelled with the pairs (1,6) (3,−12) (5,2) (7,8) (9,−4) and (11,−10). The Dowker notation for this labelling is the sequence: 6 −12 2 8 −4 −10. A knot diagram has more than one possible Dowker notation, and there is a well-understood ambiguity when reconstructing a knot from a Dowker notation.

Conway notation

Main article: Conway notation (knot theory)
The Conway notation for knots and links, named after John Horton Conway, is based on the theory of tangles (Conway 1970). The advantage of this notation is that it reflects some properties of the knot or link.
The notation describes how to construct a particular link diagram of the link. Start with a basic polyhedron, a 4-valent connected planar graph with no digon regions. Such a polyhedron is denoted first by the number of vertices then a number of asterisks which determine the polyhedron's position on a list of basic polyhedron. For example, 10** denotes the second 10-vertex polyhedron on Conway's list.
Each vertex then has an algebraic tangle substituted into it (each vertex is oriented so there is no arbitrary choice in substitution). Each such tangle has a notation consisting of numbers and + or − signs.
An example is 1*2 −3 2. The 1* denotes the only 1-vertex basic polyhedron. The 2 −3 2 is a sequence describing the continued fraction associated to a rational tangle. One inserts this tangle at the vertex of the basic polyhedron 1*.
A more complicated example is 8*3.1.2 0.1.1.1.1.1 Here again 8* refers to a basic polyhedron with 8 vertices. The periods separate the notation for each tangle.
Any link admits such a description, and it is clear this is a very compact notation even for very large crossing number. There are some further shorthands usually used. The last example is usually written 8*3:2 0, where the ones are omitted and kept the number of dots excepting the dots at the end. For an algebraic knot such as in the first example, 1* is often omitted.
Conway's pioneering paper on the subject lists up to 10-vertex basic polyhedra of which he uses to tabulate links, which have become standard for those links. For a further listing of higher vertex polyhedra, there are nonstandard choices available.

Gauss Code

Gauss Code, similar to Dowker Notation, represents a knot with a sequence of integers. However, rather than every crossing being represented by two different numbers, crossings are labeled with only one number. When the crossing is an overcrossing, a positive number is listed. At an undercrossing, a negative number.
For example, the trefoil knot in Gauss Code can be given as: 1,−2,3,−1,2,−3
Gauss Code is limited in its ability to identify knots by a few problems. The starting point on the knot at which to begin tracing the crossings is arbitrary, and there is no way to determine which direction to trace in. Also, Gauss Code is unable to indicate the handedness of each crossing, which is necessary to identify a knot versus its mirror. For example, the Gauss Code for the trefoil knot does not specify if it is the right handed or left handed trefoil.
This last issue is often solved with Extended Gauss Code. In this modification, the positive/negative sign on the second instance of every number is chosen to represent the handedness of that crossing, rather than the over/under sign of the crossing, which is made clear in the first instance of the number. A right handed crossing is given a positive number, and a left handed crossing is given a negative number

See also

References


  • Levine, J.; Orr, K (2000), "A survey of applications of surgery to knot and link theory", Surveys on Surgery Theory: Papers Dedicated to C.T.C. Wall, Annals of mathematics studies 1, Princeton University Press, ISBN 0691049386, CiteSeerX: 10.1.1.64.4359 — An introductory article to high dimensional knots and links for the advanced readers

    1. Ogasa, Eiji, Introduction to high dimensional knots, arXiv:1304.6053 — An introductory article to high dimensional knots and links for the beginners

    Further reading

    Introductory textbooks

    There are a number of introductions to knot theory. A classical introduction for graduate students or advanced undergraduates is Rolfsen (1976), given in the references. Other good texts from the references are Adams (2001) and Lickorish (1997). Adams is informal and accessible for the most part to high schoolers. Lickorish is a rigorous introduction for graduate students, covering a nice mix of classical and modern topics.

    Surveys

    External links

    Wikimedia Commons has media related to Knot theory.
    Look up knot theory in Wiktionary, the free dictionary.

    History

    Knot tables and software

    Wikimedia Commons has media related to Knot theory.
    Posted by at

    No comments:

    Post a Comment

    Subscribe to: Post Comments (Atom)