Schur polynomial
From Wikipedia, the free encyclopedia
In mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of polynomial irreducible representations of the general linear groups. The Schur polynomials form a linear basis
for the space of all symmetric polynomials. Any product of Schur
functions can be written as a linear combination of Schur polynomials
with non-negative integral coefficients; the values of these
coefficients is given combinatorially by the Littlewood–Richardson rule. More generally, skew Schur polynomials are associated with pairs of partitions and have similar properties to Schur polynomials.
Contents
Definition
Schur polynomials are indexed by integer partitions. Given a partition λ = (λ1, λ2, …,λn), where λ1 ≥ λ2≥ … ≥ λn, and each λj is a non-negative integer, the functionsSince they are alternating, they are all divisible by the Vandermonde determinant,
Properties
The degree d Schur polynomials in n variables are a linear basis for the space of homogeneous degree d symmetric polynomials in n variables. For a partition λ = (λ1, λ2, ..., λn), the Schur polynomial is a sum of monomials,Schur polynomials can be expressed as linear combinations of monomial symmetric functions mμ with non-negative integer coefficients Kλμ called Kostka numbers,
Jacobi−Trudi identities
The first Jacobi−Trudi formula expresses the Schur polynomial as a determinant in terms of the complete homogeneous symmetric polynomials,where hi := s(i).
The second Jacobi-Trudi formula expresses the Schur polynomial as a determinant in terms of the elementary symmetric polynomials,
where ei := s(1i). and λ' is the conjugate partition to λ.
These two formulae are known as determinantal identities.
The Giambelli identity
Another determinantal identity is Giambelli's formula, which expresses the Schur function for an arbitrary partition in terms of those for the hook partitions contained within the Young diagram. In Frobenius' notation, the partition is denotedThe Giambelli identity expresses the partition as the determinant
 .
.
The Cauchy identity
The Cauchy identities for the Schur functions (now in infinitely many variables), states thatThe Murnaghan−Nakayama rule
The Murnaghan–Nakayama rule expresses a product of a power-sum symmetric function with a Schur polynomial, in terms of Schur polynomials:The Littlewood-Richardson rule and Pieri's formula
The Littlewood–Richardson coefficients depend on three partitions, say , of which
, of which  and
and  describe the Schur functions being multiplied, and
describe the Schur functions being multiplied, and  gives the Schur function of which this is the coefficient in the linear combination; in other words they are the coefficients
gives the Schur function of which this is the coefficient in the linear combination; in other words they are the coefficients  such that
such that is equal to the number of Littlewood–Richardson tableaux of skew shape
is equal to the number of Littlewood–Richardson tableaux of skew shape  and of weight
and of weight  .
.Pieri's formula is a special case of the Littlewood-Richardson rule, which expresses the product
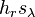 in terms of Schur polynomials.
in terms of Schur polynomials.Specializations
Evaluating the Schur polynomial sλ in (1,1,...,1) gives the number of semi-standard Young tableaux of shape λ with entries in 1, 2, ..., n. One can show, by using the Weyl character formula for example, thatExample
The following extended example should help clarify these ideas. Consider the case n = 3, d = 4. Using Ferrers diagrams or some other method, we find that there are just four partitions of 4 into at most three parts. We haveRelation to representation theory
The Schur polynomials occur in the representation theory of the symmetric groups, general linear groups, and unitary groups. The Weyl character formula implies that the Schur polynomials are the characters of finite-dimensional irreducible representations of the general linear groups, and helps to generalize Schur's work to other compact and semisimple Lie groups.Several expressions arise for this relation, one of the most important being the expansion of the Schur functions sλ in terms of the symmetric power functions
 . If we write χλ
. If we write χλρ for the character of the representation of the symmetric group indexed by the partition λ evaluated at elements of cycle type indexed by the partition ρ, then
A proof of this can be found in R. Stanley's Enumerative combinatoric II, Corollary 7.17.5.
The integers χλ
ρ can be computed using the Murnaghan–Nakayama rule.
Skew Schur functions
Skew Schur functions sλ/μ depend on two partitions λ and μ, and can be defined by the property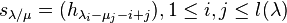 ,
,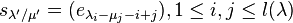 .
.
 .
.The skew Schur polynomials expands positively in Schur polynomials. A rule for the coefficients is given by the Littlewood-Richardson rule.
Generalizations
There are numerous generalizations of Schur polynomials:- Hall–Littlewood polynomials
- Shifted Schur polynomials
- Factorial Schur polynomials
- Flagged Schur polynomials
- Double Schur polynomials
- Schubert polynomials
- Stanley symmetric functions (also known as stable Schubert polynomials)
- Key polynomials (also known as Demazure characters)
- Quasi-symmetric Schur polynomials
- Jack polynomials
- Modular Schur polynomials
- Macdonald polynomials
- Schur polynomials for the symplectic and orthogonal group.
- k-Schur functions
- Loop Schur functions
- Grothendieck polynomials (K-theoretical analogue of Schur polynomials)
- LLT polynomials
Double Schur polynomials
The double Schur polynomials[3] can be seen as a generalization of the shifted Schur polynomials. These polynomials are also closely related to the factorial Schur polynomials. Given a parititon λ, and a sequence a1, a2,… one can define the double Schur polynomial sλ(x || a) asA combinatorial rule for the Littlewood-Richardson coefficients (depending on the sequence a), is given by A.I Molev in.[3] In particular, this implies that the shifted Schur polynomials have non-negative Littlewood-Richardson coefficients.
The shifted Schur polynomials, s*λ(y) , can be obtained from the double Schur polynomials by specializing ai=-i and yi=xi+i.
The double Schur polynomials are special cases of the double Schubert polynomials.
Factorial Schur polynomials
The factorial Schur polynomials may be defined as follows. Given a partiton λ, and a doubly infinite sequence …,a-1, a0, a1, … one can define the factorial Schur polynomial sλ(x|a) asThere is also a determinant formula,
The double Schur polynomials and the factorial Schur polynomials in n variables are related via the identity sλ(x||a) = sλ(x|u) where an-i+1 = ui.
![a_{(\lambda_1+n-1, \lambda_2+n-2, \dots , \lambda_n)} (x_1, x_2, \dots , x_n) =
\det \left[ \begin{matrix} x_1^{\lambda_1+n-1} & x_2^{\lambda_1+n-1} & \dots & x_n^{\lambda_1+n-1} \\
x_1^{\lambda_2+n-2} & x_2^{\lambda_2+n-2} & \dots & x_n^{\lambda_2+n-2} \\
\vdots & \vdots & \ddots & \vdots \\
x_1^{\lambda_n} & x_2^{\lambda_n} & \dots & x_n^{\lambda_n} \end{matrix} \right]](https://upload.wikimedia.org/math/d/6/1/d61d13a403edf6d6d4b2186831678423.png)
![a_{(n-1, n-2, \dots , 0)} (x_1, x_2, \dots , x_n) = \det \left[ \begin{matrix} x_1^{n-1} & x_2^{n-1} & \dots & x_n^{n-1} \\
x_1^{n-2} & x_2^{n-2} & \dots & x_n^{n-2} \\
\vdots & \vdots & \ddots & \vdots \\
1 & 1 & \dots & 1 \end{matrix} \right] = \prod_{1 \leq j < k \leq n} (x_j-x_k).](https://upload.wikimedia.org/math/f/6/0/f60590baa165de2197c288f77fbd9e82.png)










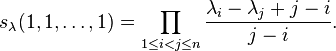
![s_{(2,1,1)} (x_1, x_2, x_3) = \frac{1}{\Delta} \;
\det \left[ \begin{matrix} x_1^4 & x_2^4 & x_3^4 \\ x_1^2 & x_2^2 & x_3^2 \\ x_1 & x_2 & x_3 \end{matrix}
\right] = x_1 \, x_2 \, x_3 \, (x_1 + x_2 + x_3)](https://upload.wikimedia.org/math/a/8/1/a817b859e59adc8c4809afaf3ef582a4.png)
![s_{(2,2,0)} (x_1, x_2, x_3) = \frac{1}{\Delta} \;
\det \left[ \begin{matrix} x_1^4 & x_2^4 & x_3^4 \\ x_1^3 & x_2^3 & x_3^3 \\ 1 & 1 & 1 \end{matrix}
\right]= x_1^2 \, x_2^2 + x_1^2 \, x_3^2 + x_2^2 \, x_3^2
+ x_1^2 \, x_2 \, x_3 + x_1 \, x_2^2 \, x_3 + x_1 \, x_2 \, x_3^2](https://upload.wikimedia.org/math/7/e/2/7e209a9f378b764c8a1c42f837578c63.png)

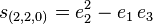








![s_\lambda(x|a) = \frac{\det[(x_j|a)^{\lambda_i+n-i}]_{1\leq i,j\leq n}}{\prod_{i<j}(x_i-x_j)}](https://upload.wikimedia.org/math/b/9/6/b965430afb8f9ff608763f0c787ede3c.png)
No comments:
Post a Comment