Lorentz group
From Wikipedia, the free encyclopedia
Hendrik Antoon Lorentz (1853–1928), after whom the Lorentz group is named.
Under the Lorentz transformations, these laws and equations are invariant:
- The kinematical laws of special relativity
- Maxwell's field equations in the theory of electromagnetism
- The Dirac equation in the theory of the electron
Contents
Basic properties
The Lorentz group is a subgroup of the Poincaré group—the group of all isometries of Minkowski spacetime. Lorentz transformations are, precisely, isometries that leave the origin fixed. Thus, the Lorentz group is an isotropy subgroup of the isometry group of Minkowski spacetime. For this reason, the Lorentz group is sometimes called the homogeneous Lorentz group while the Poincaré group is sometimes called the inhomogeneous Lorentz group. Lorentz transformations are examples of linear transformations; general isometries of Minkowski spacetime are affine transformations. Mathematically, the Lorentz group may be described as the generalized orthogonal group O(1,3), the matrix Lie group that preserves the quadratic formThe Lorentz group is a six-dimensional noncompact non-abelian real Lie group that is not connected. All four of its connected components are not simply connected. The identity component (i.e., the component containing the identity element) of the Lorentz group is itself a group, and is often called the restricted Lorentz group, and is denoted SO+(1,3). The restricted Lorentz group consists of those Lorentz transformations that preserve the orientation of space and direction of time. The restricted Lorentz group has often been presented through a facility of biquaternion algebra.
The restricted Lorentz group arises in other ways in pure mathematics. For example, it arises as the point symmetry group of a certain ordinary differential equation. This fact also has physical significance.
Connected components
Light cone in 2D space plus a time dimension.
Each of the four connected components can be categorized by which of these two properties its elements have:
- The element reverses the direction of time, or more precisely, transforms a future-pointing timelike vector into a past-pointing one.
- The element reverses the orientation of a vierbein (tetrad).
The subgroup of all Lorentz transformations preserving both orientation and direction of time is called the proper, orthochronous Lorentz group or restricted Lorentz group, and is denoted by SO+(1, 3). (Note that some authors refer to SO(1,3) or even O(1,3) when they actually mean SO+(1, 3).)
The set of the four connected components can be given a group structure as the quotient group O(1,3)/SO+(1,3), which is isomorphic to the Klein four-group. Every element in O(1,3) can be written as the semidirect product of a proper, orthochronous transformation and an element of the discrete group
- {1, P, T, PT}
- P = diag(1, −1, −1, −1)
- T = diag(−1, 1, 1, 1).
Restricted Lorentz group
The restricted Lorentz group is the identity component of the Lorentz group, which means that it consists of all Lorentz transformations that can be connected to the identity by a continuous curve lying in the group. The restricted Lorentz group is a connected normal subgroup of the full Lorentz group with the same dimension, in this case with dimension six.The restricted Lorentz group is generated by ordinary spatial rotations and Lorentz boosts (which can be thought of as hyperbolic rotations in a plane that includes a time-like direction). Since every proper, orthochronous Lorentz transformation can be written as a product of a rotation (specified by 3 real parameters) and a boost (also specified by 3 real parameters), it takes 6 real parameters to specify an arbitrary proper orthochronous Lorentz transformation. This is one way to understand why the restricted Lorentz group is six-dimensional. (See also the Lie algebra of the Lorentz group.)
The set of all rotations forms a Lie subgroup isomorphic to the ordinary rotation group SO(3). The set of all boosts, however, does not form a subgroup, since composing two boosts does not, in general, result in another boost. (Rather, a pair of non-colinear boosts is equivalent to a boost and a rotation, and this relates to Thomas rotation.) A boost in some direction, or a rotation about some axis, generates a one-parameter subgroup.
Surfaces of transitivity
 Hyperboloid of one sheet |
 Common conical surface |
 Hyperboloid of two sheets |
- Q(x) > 0, x0 > 0 is the upper branch of a hyperboloid of two sheets.
- Q(x) > 0, x0 < 0 is the lower branch of this hyperboloid.
- Q(x) = 0, x0 > 0 is the upper branch of the light cone.
- Q(x) = 0, x0 < 0 is the lower branch of the light cone.
- Q(x) < 0 is a hyperboloid of one sheet.
- The origin x0 = x1 = x2 = x3 = 0.
These observations constitute a good starting point for finding all infinite-dimensional unitary representations of the Lorentz group, in fact, of the Poincaré group, using the method of induced representations.[2] One begins with a "standard vector", one for each surface of transitivity, and then ask which subgroup preserves these vectors. These subgroups are called little groups by physicists. The problem is then essentially reduced to the easier problem of finding representations of the little groups. For example, a standard vector in one of the hyperbolas of two sheets could be suitably chosen as (m, 0, 0, 0). For each m ≠ 0, the vector pierces exactly one sheet. In this case the little group is SO(3), the rotation group, all of whose representations are known. The precise infinite-dimensional unitary representation under which a particle transform is part of its classification. Not all representations can correspond to physical particles (as far as is known). Standard vectors on the one-sheeted hyperbolas would correspond to tachyons. Particles on the light cone are photons, and more hypothetically, gravitons. The "particle" corresponding to the origin is the vacuum.
Relation to the Möbius group
| Algebraic structure → Group theory Group theory |
|---|
 |
See also: Algebra of physical space
The restricted Lorentz group SO+(1, 3) is isomorphic to the projective special linear group PSL(2,C), which is in turn isomorphic to the Möbius group, the symmetry group of conformal geometry on the Riemann sphere. (This observation was utilized by Roger Penrose as the starting point of twistor theory.)This may be shown by constructing a surjective homomorphism of Lie groups from SL(2,C) to SO+(1,3), which we will call the spinor map. This proceeds as follows:
We can define an action of SL(2,C) on Minkowski spacetime by writing a point of spacetime as a two-by-two Hermitian matrix in the form
 is the Hermitian transpose of
is the Hermitian transpose of 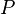 , and this action preserves the determinant. Therefore, SL(2,C)
acts on Minkowski spacetime by (linear) isometries, and so is
homomorphic to a subgroup of the Lorentz group (by the definition of the
Lorentz group.)
, and this action preserves the determinant. Therefore, SL(2,C)
acts on Minkowski spacetime by (linear) isometries, and so is
homomorphic to a subgroup of the Lorentz group (by the definition of the
Lorentz group.)This completes the proof that there is a homomorphism from SL(2,C) to SO+(1,3). The kernel of the spinor map is the two element subgroup ±I, and it happens that the map is surjective. By the first isomorphism theorem, the quotient group PSL(2,C) is isomorphic to SO+(1,3).
In optics, this construction is known as the Poincaré sphere.
Appearance of the night sky
| Group theory → Lie groups Lie groups |
|---|
 |
Suppose the "fixed stars" live in Minkowski spacetime and are modeled by points on the celestial sphere. Then a given point on the celestial sphere can be associated with ξ = u + iv, a complex number that corresponds to the point on the Riemann sphere, and can be identified with a null vector (a light-like vector) in Minkowski space
Conjugacy classes
Because the restricted Lorentz group SO+(1, 3) is isomorphic to the Möbius group PSL(2,C), its conjugacy classes also fall into five classes:- Elliptic transformations
- Hyperbolic transformations
- Loxodromic transformations
- Parabolic transformations
- The trivial identity transformation
An example of each type is given in the subsections below, along with the effect of the one-parameter subgroup it generates (e.g., on the appearance of the night sky).
The Möbius transformations are the conformal transformations of the Riemann sphere (or celestial sphere). Then conjugating with an arbitrary element of SL(2,C) obtains the following examples of arbitrary elliptic, hyperbolic, loxodromic, and parabolic (restricted) Lorentz transformations, respectively. The effect on the flow lines of the corresponding one-parameter subgroups is to transform the pattern seen in the examples by some conformal transformation. For example, an elliptic Lorentz transformation can have any two distinct fixed points on the celestial sphere, but points still flow along circular arcs from one fixed point toward the other. The other cases are similar.
Elliptic
An elliptic element of SL(2,C) isThe corresponding continuous transformations of the celestial sphere (except for the identity) all share the same two fixed points, the North and South poles. The transformations move all other points around latitude circles so that this group yields a continuous counterclockwise rotation about the z axis as θ increases. The angle doubling evident in the spinor map is a characteristic feature of spinorial double coverings.
Hyperbolic
A hyperbolic element of SL(2,C) isThe spinor map converts this to the Lorentz transformation
Loxodromic
A loxodromic element of SL(2,C) isThe corresponding continuous transformations of the celestial sphere (excepting the identity) all share the same two fixed points (the North and South poles). They move all other points away from the South pole and toward the North pole (or vice versa), along a family of curves called loxodromes. Each loxodrome spirals infinitely often around each pole.
Parabolic
A parabolic element of SL(2,C) isThe spinor map converts this to the matrix (representing a Lorentz transformation)
Parabolic Lorentz transformations are often called null rotations, since they preserve null vectors, just as rotations preserve timelike vectors and boosts preserve spacelike vectors. Since these are likely to be the least familiar of the four types of nonidentity Lorentz transformations (elliptic, hyperbolic, loxodromic, parabolic), it is illustrated here how to determine the effect of an example of a parabolic Lorentz transformation on Minkowski spacetime.
The matrix given above yields the transformation
The form of the rational invariants shows that these flowlines (orbits) have a simple description: suppressing the inessential coordinate y, each orbit is the intersection of a null plane, t = z+c2, with a hyperboloid, t2−x2−z2 = c3. The case c3 = 0 has the hyperboloid degenerate to a light cone with the orbits becoming parabolas lying in corresponding null planes.
A particular null line lying on the light cone is left invariant; this corresponds to the unique (double) fixed point on the Riemann sphere mentioned above. The other null lines through the origin are "swung around the cone" by the transformation. Following the motion of one such null line as α increases corresponds to following the motion of a point along one of the circular flow lines on the celestial sphere, as described above.
A choice Re(α)=0 instead, produces similar orbits, now with the roles of x and y interchanged.
Parabolic transformations lead to the gauge symmetry of massless particles (like photons) with helicity |h| ≥ 1. In the above explicit example, a massless particle moving in the z direction, so with 4-momentum P=(p,0,0,p), is not affected at all by the x-boost and y-rotation combination Kx−Jy displayed above, in the "little group" of its motion. This is evident from the explicit transformation law discussed: like any light-like vector, P itself is now invariant, i.e., all traces or effects of α have disappeared. c1 = c2 = c3 = 0, in the special case discussed. (The other similar generator, Ky+Jx as well as it and Jz comprise altogether the little group of the lightlike vector, isomorphic to E(2).)
Lie algebra
As with any Lie group, the best way to study many aspects of the Lorentz group is via its Lie algebra. The Lorentz group is a subgroup of the diffeomorphism group of R4 and therefore its Lie algebra can be identified with vector fields on R4. In particular, the vectors that generate isometries on a space are its Killing vectors, which provides a convenient alternative to the left-invariant vector field for calculating the Lie algebra. We can write down a set of six generators:- vector fields on R4 generating three rotations i J,
- vector fields on R4 generating three boosts i K,
Reversing the procedure in the previous section, we see that the Möbius transformations that correspond to our six generators arise from exponentiating respectively β/2 (for the three boosts) or iθ/2 (for the three rotations) times the three Pauli matrices
- The first column gives a generator of the flow under the Möbius action (after stereographic projection from the Riemann sphere) as a real vector field on the Euclidean plane.
- The second column gives the corresponding one-parameter subgroup of Möbius transformations.
- The third column gives the corresponding one-parameter subgroup of Lorentz transformations (the image under our homomorphism of preceding one-parameter subgroup).
- The fourth column gives the corresponding generator of the flow under the Lorentz action as a real vector field on Minkowski spacetime.
- Two parabolics (null rotations)
- One hyperbolic (boost in the ∂z direction)
- Three elliptics (rotations about the x,y,z axes, respectively)
| Vector field on R2 | One-parameter subgroup of SL(2,C), representing Möbius transformations |
One-parameter subgroup of SO+(1,3), representing Lorentz transformations |
Vector field on R4 |
|---|---|---|---|
| Parabolic | |||
 |
![\left[ \begin{matrix} 1 & \alpha \\ 0 & 1 \end{matrix} \right]](https://upload.wikimedia.org/math/1/6/f/16f4bb8776d0cb885bd712b20d9353d4.png) |
![\left[ \begin{matrix} 1+\alpha^2/2 & \alpha & 0 & -\alpha^2/2 \\
\alpha & 1 & 0 & -\alpha \\
0 & 0 & 1 & 0 \\
\alpha^2/2 & \alpha & 0 & 1-\alpha^2/2 \end{matrix} \right]](https://upload.wikimedia.org/math/8/e/3/8e3d3ceb3e0bf3ff1d5f32b370a887a3.png) |
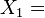  |
 |
![\left[ \begin{matrix} 1 & i \alpha \\ 0 & 1 \end{matrix} \right]](https://upload.wikimedia.org/math/5/7/3/5732e6441eeec1f408ec46ef26bc768b.png) |
![\left[ \begin{matrix} 1+\alpha^2/2 & 0 & \alpha & -\alpha^2/2 \\
0 & 1 & 0 & 0 \\
\alpha & 0 & 1 & -\alpha \\
\alpha^2/2 & 0 & \alpha & 1-\alpha^2/2 \end{matrix} \right]](https://upload.wikimedia.org/math/e/d/d/edd8a20f5baeff578ac33fbd8514a52d.png) |
 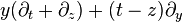 |
| Hyperbolic | |||
 |
![\left[ \begin{matrix} \exp \left(\frac{\beta}{2}\right) & 0 \\
0 & \exp \left(-\frac{\beta}{2}\right) \end{matrix} \right]](https://upload.wikimedia.org/math/f/2/b/f2b27bf02ed71bbcdfdd57af8c002d5e.png) |
![\left[ \begin{matrix} \cosh(\beta) & 0 & 0 & \sinh(\beta) \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
\sinh(\beta) & 0 & 0 & \cosh(\beta) \end{matrix} \right]](https://upload.wikimedia.org/math/a/b/1/ab1db11fb9e672abac96c1ff2964ad9f.png) |
  |
| Elliptic | |||
 |
![\left[ \begin{matrix} \exp \left( \frac{i \theta}{2} \right) & 0 \\
0 & \exp \left( \frac{-i \theta}{2} \right) \end{matrix} \right]](https://upload.wikimedia.org/math/a/4/a/a4ad46bae8a3140b9020cca869051f46.png) |
![\left[ \begin{matrix} 1 & 0 & 0 & 0 \\
0 & \cos(\theta) & -\sin(\theta) & 0 \\
0 & \sin(\theta) & \cos(\theta) & 0 \\
0 & 0 & 0 & 1 \end{matrix} \right]](https://upload.wikimedia.org/math/0/0/f/00fe46f7e38ef9867d334294f3191032.png) |
 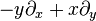 |
 |
![\left[ \begin{matrix} \cos \left( \frac{\theta}{2} \right) & -\sin \left( \frac{\theta}{2} \right) \\
\sin \left( \frac{\theta}{2} \right) & \cos \left( \frac{\theta}{2} \right) \end{matrix} \right]](https://upload.wikimedia.org/math/b/0/8/b08a6aaa8139a6e43f172325c384f5a8.png) |
![\left[ \begin{matrix} 1 & 0 & 0 & 0 \\
0 & \cos(\theta) & 0 & \sin(\theta) \\
0 & 0 & 1 & 0 \\
0 & -\sin(\theta) & 0 & \cos(\theta) \end{matrix} \right]](https://upload.wikimedia.org/math/2/4/2/2423543abc957904b3135f932f0788e0.png) |
 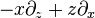 |
 |
![\left[ \begin{matrix} \cos \left( \frac{\theta}{2} \right) & i \sin \left( \frac{\theta}{2} \right) \\
i \sin \left( \frac{\theta}{2} \right) & \cos \left( \frac{\theta}{2} \right) \end{matrix} \right]](https://upload.wikimedia.org/math/5/8/1/58117bb8dccba8522ce6beea2f65b74e.png) |
![\left[ \begin{matrix} 1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & \cos(\theta) & -\sin(\theta) \\
0 & 0 & \sin(\theta) & \cos(\theta) \end{matrix} \right]](https://upload.wikimedia.org/math/9/f/f/9ff6590cd46afec1c370d8d04b1ac567.png) |
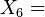  |
 , this becomes the vector field on R2
, this becomes the vector field on R2 and collecting terms, we find that the image under the spinor map is the element of SO+(1,3)
and collecting terms, we find that the image under the spinor map is the element of SO+(1,3)Subgroups of the Lorentz group
The subalgebras of the Lie algebra of the Lorentz group can be enumerated, up to conjugacy, from which we can list the closed subgroups of the restricted Lorentz group, up to conjugacy. (See the book by Hall cited below for the details.) We can readily express the result in terms of the generating set given in the table above.The one-dimensional subalgebras of course correspond to the four conjugacy classes of elements of the Lorentz group:
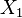 generates a one-parameter subalgebra of parabolics SO(0,1),
generates a one-parameter subalgebra of parabolics SO(0,1), generates a one-parameter subalgebra of boosts SO(1,1),
generates a one-parameter subalgebra of boosts SO(1,1), generates a one-parameter of rotations SO(2),
generates a one-parameter of rotations SO(2), (for any
(for any 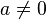 ) generates a one-parameter subalgebra of loxodromic transformations.
) generates a one-parameter subalgebra of loxodromic transformations.
 give different classes.) The two-dimensional subalgebras are:
give different classes.) The two-dimensional subalgebras are: generate an abelian subalgebra consisting entirely of parabolics,
generate an abelian subalgebra consisting entirely of parabolics, generate a nonabelian subalgebra isomorphic to the Lie algebra of the affine group A(1),
generate a nonabelian subalgebra isomorphic to the Lie algebra of the affine group A(1), generate an abelian subalgebra consisting of boosts, rotations, and loxodromics all sharing the same pair of fixed points.
generate an abelian subalgebra consisting of boosts, rotations, and loxodromics all sharing the same pair of fixed points.
 generate a Bianchi V subalgebra, isomorphic to the Lie algebra of Hom(2), the group of euclidean homotheties,
generate a Bianchi V subalgebra, isomorphic to the Lie algebra of Hom(2), the group of euclidean homotheties,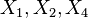 generate a Bianchi VII_0 subalgebra, isomorphic to the Lie algebra of E(2), the euclidean group,
generate a Bianchi VII_0 subalgebra, isomorphic to the Lie algebra of E(2), the euclidean group, , where
, where 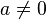 , generate a Bianchi VII_a subalgebra,
, generate a Bianchi VII_a subalgebra,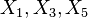 generate a Bianchi VIII subalgebra, isomorphic to the Lie algebra of SL(2,R), the group of isometries of the hyperbolic plane,
generate a Bianchi VIII subalgebra, isomorphic to the Lie algebra of SL(2,R), the group of isometries of the hyperbolic plane,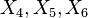 generate a Bianchi IX subalgebra, isomorphic to the Lie algebra of SO(3), the rotation group.
generate a Bianchi IX subalgebra, isomorphic to the Lie algebra of SO(3), the rotation group.
 generate a subalgebra isomorphic to the Lie algebra of Sim(2), the group of Euclidean similitudes.
generate a subalgebra isomorphic to the Lie algebra of Sim(2), the group of Euclidean similitudes.
The lattice of subalgebras of the Lie algebra SO(1,3), up to conjugacy.
- The group Sim(2) is the stabilizer of a null line, i.e., of a point on the Riemann sphere—so the homogeneous space SO+(1,3)/Sim(2) is the Kleinian geometry that represents conformal geometry on the sphere S.2
- The (identity component of the) Euclidean group SE(2) is the stabilizer of a null vector, so the homogeneous space SO+(1,3)/SE(2) is the momentum space of a massless particle; geometrically, this Kleinian geometry represents the degenerate geometry of the light cone in Minkowski spacetime.
- The rotation group SO(3) is the stabilizer of a timelike vector, so the homogeneous space SO+(1,3)/SO(3) is the momentum space of a massive particle; geometrically, this space is none other than three-dimensional hyperbolic space H3.
Covering groups
In a previous section, we constructed a homomorphism SL(2, C) → SO+(1, 3), which we called the spinor map. Since SL(2,C) is simply connected, it is the covering group of the restricted Lorentz group SO+(1, 3). By restriction we obtain a homomorphism SU(2) → SO(3). Here, the special unitary group SU(2), which is isomorphic to the group of unit norm quaternions, is also simply connected, so it is the covering group of the rotation group SO(3). Each of these covering maps are twofold covers in the sense that precisely two elements of the covering group map to each element of the quotient. One often says that the restricted Lorentz group and the rotation group are doubly connected. This means that the fundamental group of the each group is isomorphic to the two-element cyclic group Z2.(In applications to quantum mechanics, the special linear group SL(2, C) is sometimes called the Lorentz group.)
Twofold coverings are characteristic of spin groups. Indeed, in addition to the double coverings
- Spin+(1, 3) = SL(2, C) → SO+(1, 3)
- Spin(3) = SU(2) → SO(3)
- Pin(1, 3) → O(1, 3)
- Spin(1, 3) → SO(1, 3)
- Spin+(1, 2) = SU(1, 1) → SO(1, 2)
Topology
The left and right groups in the double covering- SU(2) → SO(3)
- SL(2,C) → SO+(1,3).
Generalization to higher dimensions
The concept of the Lorentz group has a natural generalization to spacetime of any number of dimensions. Mathematically, the Lorentz group of n+1-dimensional Minkowski space is the group O(n,1) (or O(1,n)) of linear transformations of Rn+1 that preserves the quadratic formThe low-dimensional cases n = 1 and n = 2 are often useful as "toy models" for the physical case n = 3, while higher-dimensional Lorentz groups are used in physical theories such as string theory that posit the existence of hidden dimensions. The Lorentz group O(n,1) is also the isometry group of n-dimensional de Sitter space dSn, which may be realized as the homogeneous space O(n,1)/O(n−1,1). In particular O(4,1) is the isometry group of the de Sitter universe dS4, a cosmological model.
Notes
See also
References
- Artin, Emil (1957). Geometric Algebra. New York: Wiley. ISBN 0-471-60839-4. See Chapter III for the orthogonal groups O(p,q).
- Carmeli, Moshe (1977). Group Theory and General Relativity, Representations of the Lorentz Group and Their Applications to the Gravitational Field. McGraw-Hill, New York. ISBN 0-07-009986-3. A canonical reference; see chapters 1–6 for representations of the Lorentz group.
- Frankel, Theodore (2004). The Geometry of Physics (2nd Ed.). Cambridge: Cambridge University Press. ISBN 0-521-53927-7. An excellent resource for Lie theory, fiber bundles, spinorial coverings, and many other topics.
- Fulton, William; Harris, Joe (1991), Representation theory. A first course, Graduate Texts in Mathematics, Readings in Mathematics 129, New York: Springer-Verlag, ISBN 978-0-387-97495-8, MR 1153249, ISBN 978-0-387-97527-6 See Lecture 11 for the irreducible representations of SL(2,C).
- Gelfand, I.M.; Minlos, R.A.; Shapiro, Z.Ya. (1963), Representations of the Rotation and Lorentz Groups and their Applications, New York: Pergamon Press
- Hall, G. S. (2004). Symmetries and Curvature Structure in General Relativity. Singapore: World Scientific. ISBN 981-02-1051-5. See Chapter 6 for the subalgebras of the Lie algebra of the Lorentz group.
- Hatcher, Allen (2002). Algebraic topology. Cambridge: Cambridge University Press. ISBN 0-521-79540-0. See also the "online version". Retrieved July 3, 2005. See Section 1.3 for a beautifully illustrated discussion of covering spaces. See Section 3D for the topology of rotation groups.
- Naber, Gregory (1992). The Geometry of Minkowski Spacetime. New York: Springer-Verlag. ISBN 0486432351. (Dover reprint edition.) An excellent reference on Minkowski spacetime and the Lorentz group.
- Needham, Tristan (1997). Visual Complex Analysis. Oxford: Oxford University Press. ISBN 0-19-853446-9. See Chapter 3 for a superbly illustrated discussion of Möbius transformations.
- Wigner, E. P. (1939), "On unitary representations of the inhomogeneous Lorentz group", Annals of Mathematics 40 (1): 149–204, Bibcode:1939AnMat..40..922E, doi:10.2307/1968551, MR 1503456.




![X = \left[ \begin{matrix} t+z & x-iy \\ x+iy & t-z \end{matrix} \right].](https://upload.wikimedia.org/math/3/2/7/327e13d9b2916e8d05ea133fb43a6264.png)

![\left[ \begin{matrix} u^2+v^2+1 \\ 2u \\ -2v \\ u^2+v^2-1 \end{matrix} \right]](https://upload.wikimedia.org/math/6/8/2/682d891214ee3f198b5f73b1309e0912.png)
![N = 2\left[ \begin{matrix} u^2+v^2 & u+iv \\ u-iv & 1 \end{matrix} \right].](https://upload.wikimedia.org/math/6/5/c/65cad2dc17ba049dcf478ca95c0a65b9.png)
![P_1 = \left[ \begin{matrix} \exp(i \theta/2) & 0 \\ 0 & \exp(-i \theta/2) \end{matrix} \right]](https://upload.wikimedia.org/math/7/0/0/700a9050b375b155d8ed11ff3768b5ee.png)
![Q_1 = \left[ \begin{matrix} 1 & 0 & 0 & 0 \\
0 & \cos(\theta) & -\sin(\theta) & 0 \\
0 & \sin(\theta) & \cos(\theta) & 0 \\
0 & 0 & 0 & 1 \end{matrix} \right]=\exp \left ( \theta
\left[ \begin{matrix} 0 & 0 & 0 & 0 \\
0 & 0 & -1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 \end{matrix} \right]
\right ) ~.](https://upload.wikimedia.org/math/c/5/8/c584af85b78ebc743f08908211755069.png)
![P_2 = \left[ \begin{matrix} \exp(\beta/2) & 0 \\ 0 & \exp(-\beta/2) \end{matrix} \right]](https://upload.wikimedia.org/math/3/1/9/31939132297e6fd5761f797959238b74.png)
![Q_2 = \left[ \begin{matrix} \cosh(\beta) & 0 & 0 & \sinh(\beta) \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
\sinh(\beta) & 0 & 0 & \cosh(\beta) \end{matrix} \right] = \exp \left ( \beta\left[ \begin{matrix}
0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0
\end{matrix} \right] \right )~.](https://upload.wikimedia.org/math/4/4/f/44f60c0fa451ea1b3577e50ca64a83dd.png)
![P_3 = P_2 P_1 = P_1 P_2
= \left[ \begin{matrix} \exp \left((\beta+i\theta)/2 \right) & 0 \\
0 & \exp \left(-(\beta+i\theta)/2 \right)
\end{matrix} \right]](https://upload.wikimedia.org/math/9/c/1/9c16dc2bfffa9350fd8482f7d86c2b30.png)

![P_4 = \left[ \begin{matrix} 1 & \alpha \\ 0 & 1 \end{matrix} \right]](https://upload.wikimedia.org/math/e/c/6/ec66198fab2f9dbf6a9538bc3a130024.png)
![Q_4 = \left[ \begin{matrix} 1+\vert\alpha\vert^2/2 & \operatorname{Re}(\alpha) & \operatorname{Im}(\alpha) & -\vert\alpha\vert^2/2 \\
\operatorname{Re}(\alpha) & 1 & 0 & -\operatorname{Re}(\alpha) \\
-\operatorname{Im}(\alpha) & 0 & 1 & \operatorname{Im}(\alpha) \\
\vert\alpha\vert^2/2 & \operatorname{Re}(\alpha) & \operatorname{Im}(\alpha) & 1-\vert\alpha\vert^2/2 \end{matrix} \right]](https://upload.wikimedia.org/math/5/1/3/513d6e4232daad0dec3031a6ab182edc.png)
![~ = \exp \left[ \begin{matrix} 0& \operatorname{Re}(\alpha) & \operatorname{Im}(\alpha) & 0 \\
\operatorname{Re}(\alpha) & 0 & 0 & -\operatorname{Re}(\alpha) \\
-\operatorname{Im}(\alpha) & 0 & 0 & \operatorname{Im}(\alpha) \\
0 & \operatorname{Re}(\alpha) & \operatorname{Im}(\alpha) & 0 \end{matrix} \right] ~ .](https://upload.wikimedia.org/math/5/8/f/58f959315488af9380634ff8658cc564.png)
![\left[ \begin{matrix} t \\ x \\ y \\ z \end{matrix} \right]
\rightarrow
\left[ \begin{matrix} t \\ x \\ y \\ z \end{matrix} \right]
+ \operatorname{Re}(\alpha) \;
\left[ \begin{matrix} x \\ t-z \\ 0 \\ x \end{matrix} \right]
+ \operatorname{Im}(\alpha) \;
\left[ \begin{matrix} y \\ 0 \\ z-t \\ y \end{matrix} \right]
+ \frac{\vert\alpha\vert^2}{2} \;
\left[ \begin{matrix} t-z \\ 0 \\ 0 \\ t-z \end{matrix} \right].](https://upload.wikimedia.org/math/0/e/8/0e87646b35a83470cd19adfc80bc07f0.png)



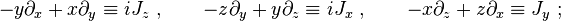

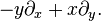


![\left[ \begin{matrix} t \\ x \\ y \\ z \end{matrix} \right]
= \left[ \begin{matrix} 1 & 0 & 0 & 0 \\
0 & \cos(\lambda) & -\sin(\lambda) & 0 \\
0 & \sin(\lambda) & \cos(\lambda) & 0 \\
0 & 0 & 0 & 1 \end{matrix} \right]
\left[ \begin{matrix} t_0 \\ x_0 \\ y_0 \\ z_0 \end{matrix} \right]](https://upload.wikimedia.org/math/a/2/6/a269d15e50456595281ce86b33f95901.png)
![iJ_z= \left[ \begin{matrix} 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{matrix} \right] ~,](https://upload.wikimedia.org/math/b/6/2/b625f667a93868d77a1f61c53b3bf071.png)
![\sigma_1 = \left[ \begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix} \right], \; \;
\sigma_2 = \left[ \begin{matrix} 0 & -i \\ i & 0 \end{matrix} \right], \; \;
\sigma_3 = \left[ \begin{matrix} 1 & 0 \\ 0 & -1 \end{matrix} \right].](https://upload.wikimedia.org/math/0/1/a/01a0210b0f8eecd2867fd20c225be64b.png)
![\sigma_2 = \left[ \begin{matrix} 0 & i \\ -i & 0 \end{matrix} \right].](https://upload.wikimedia.org/math/f/0/f/f0f47ab2d810b8dddd6ed2b6a50728c7.png)
![\exp \left( \frac{ i \theta}{2} \, \sigma_2 \right) =
\left[ \begin{matrix} \cos(\theta/2) & -\sin(\theta/2) \\ \sin(\theta/2) & \cos(\theta/2) \end{matrix} \right].](https://upload.wikimedia.org/math/f/f/2/ff2d615886ea7079dcb8a19b1d37f17b.png)

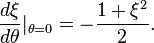

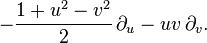
![\left[ \begin{matrix} 1 & 0 & 0 & 0 \\
0 & \cos(\theta) & 0 & \sin(\theta) \\
0 & 0 & 1 & 0 \\
0 & -\sin(\theta) & 0 & \cos(\theta) \end{matrix} \right].](https://upload.wikimedia.org/math/f/a/e/faef5eae39908298ac55c6b6cd155617.png)

No comments:
Post a Comment