Electric dipole spin resonance
From Wikipedia, the free encyclopedia
|
|
This article may be too technical for most readers to understand. (August 2015) |
 and magnetic moment
and magnetic moment  whose absolute value equals to the Bohr magneton
whose absolute value equals to the Bohr magneton 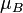 . Contemporary computational techniques employ electron charge in transistors to process information and electron spin in magnetic storage devices to accumulate it. The emergent field of spintronics
aims in unifying operations of these subsystems. For achieving this
goal, electron spin should be operated by electric fields, and electric dipole spin resonance (EDSR) is one of the most efficient tools for achieving this goal. It allows performing spin flip transitions by resonant
. Contemporary computational techniques employ electron charge in transistors to process information and electron spin in magnetic storage devices to accumulate it. The emergent field of spintronics
aims in unifying operations of these subsystems. For achieving this
goal, electron spin should be operated by electric fields, and electric dipole spin resonance (EDSR) is one of the most efficient tools for achieving this goal. It allows performing spin flip transitions by resonant  electric fields.
electric fields.Contents
Theory
Electron spin resonance, also known as electron paramagnetic resonance, is due to the coupling of electron magnetic moment to the external magnetic field
to the external magnetic field 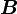 through the Hamiltonian
through the Hamiltonian  describing its Larmor precession. Magnetic moment
describing its Larmor precession. Magnetic moment  is related to electron angular momentum
is related to electron angular momentum  as
as  , where
, where  is a Landé g-factor. For a free electron in vacuum
is a Landé g-factor. For a free electron in vacuum  . Larmor interaction quantizes electron spin energy levels in a dc magnetic field
. Larmor interaction quantizes electron spin energy levels in a dc magnetic field  as
as  , and a resonant ac magnetic field
, and a resonant ac magnetic field  of a frequency
of a frequency  results in electron paramagnetic resonance.
results in electron paramagnetic resonance.Coupling electron spin to electric fields in vacuum and atoms
An electron moving in vacuum in an ac electric field sees, according to the Lorentz transformation, an ac magnetic field
sees, according to the Lorentz transformation, an ac magnetic field  in its center of mass system. However, for slow electrons with
in its center of mass system. However, for slow electrons with  this field is so weak that its effect can be neglected. In atoms,
electron orbital and spin dynamics are coupled because of the electric
field of nuclei as it follows from the Dirac equation. This coupling, known as spin-orbit interaction, is small in the fine-structure constant
this field is so weak that its effect can be neglected. In atoms,
electron orbital and spin dynamics are coupled because of the electric
field of nuclei as it follows from the Dirac equation. This coupling, known as spin-orbit interaction, is small in the fine-structure constant  . However, this constant appears in a combination with the atomic number
. However, this constant appears in a combination with the atomic number 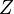 as
as  ,[1] and this product is of the order of unity already in the middle of the periodic table.
This enhancement of the coupling between the orbital and spin dynamics
originates from strong electric fields and electron velocities near
nuclei. While this mechanism is also expected to couple electron spin to
ac electric fields, such an effect has been probably never observed in atomic spectroscopy.
,[1] and this product is of the order of unity already in the middle of the periodic table.
This enhancement of the coupling between the orbital and spin dynamics
originates from strong electric fields and electron velocities near
nuclei. While this mechanism is also expected to couple electron spin to
ac electric fields, such an effect has been probably never observed in atomic spectroscopy.Basic mechanisms of Electric Dipole Spin Resonance in crystals
Most important, this enhanced spin-orbit coupling in atoms translates into spin-orbit coupling in crystals formed from such atoms or ions that may be strong even for slow electrons. It becomes an essential part of the band structure of their energy spectrum. The ratio of the spin-orbit splitting of the bands to the forbidden gap becomes a parameter that evaluates the effect of spin-orbit coupling, and it is generically of the order of unity.As a result, even slow electrons in solids experience strong spin-orbit coupling. This means that the Hamiltonian of a free electron in a crystal includes, side by side with the electron quasimomentum
 also Pauli matrices
also Pauli matrices  , and the terms including both of them are not small. Coupling of electron spin to the external electromagnetic field can be found by the substitution
, and the terms including both of them are not small. Coupling of electron spin to the external electromagnetic field can be found by the substitution  as is required by the gauge invariance of the theory, here
as is required by the gauge invariance of the theory, here  is the vector potential, and the substitution is known as Peierls substitution. And because the electric field
is the vector potential, and the substitution is known as Peierls substitution. And because the electric field  , it becomes coupled to the electron spin and can produce spin-flip transitions.
, it becomes coupled to the electron spin and can produce spin-flip transitions.Electric Dipole Spin Resonance (EDSR) is the electron spin resonance driven by a resonant ac electric field
 . Because the Compton length
. Because the Compton length  cm entering into the Bohr magneton
cm entering into the Bohr magneton  and controlling the coupling of electron spin to ac magnetic field
and controlling the coupling of electron spin to ac magnetic field  is much shorter than all characteristic lengths of solid state physics, EDSR can be by orders of magnitude stronger than the electron paramagnetic resonance driven by ac magnetic field. EDSR was proposed by Rashba.[2]
is much shorter than all characteristic lengths of solid state physics, EDSR can be by orders of magnitude stronger than the electron paramagnetic resonance driven by ac magnetic field. EDSR was proposed by Rashba.[2]EDSR is usually strongest in materials without the inversion center where the two-fold degeneracy of the energy spectrum is lifted and time-symmetric Hamiltonians include products of Pauli matrices
 and odd powers of the quasimomemtum
and odd powers of the quasimomemtum  . In such cases electron spin is coupled to the vector-potential
. In such cases electron spin is coupled to the vector-potential  of electromagnetic field. Remarkably, EDSR on free electrons can be observed not only at the spin-resonance frequency
of electromagnetic field. Remarkably, EDSR on free electrons can be observed not only at the spin-resonance frequency  but also at its linear combinations with the cyclotron resonance frequency
but also at its linear combinations with the cyclotron resonance frequency  . In narrow-gap semiconductors with inversion center EDSR can emerge due direct coupling of electric field
. In narrow-gap semiconductors with inversion center EDSR can emerge due direct coupling of electric field  to the anomalous coordinate
to the anomalous coordinate  , see Spin-orbit interaction.
, see Spin-orbit interaction.EDSR is allowed both with free carriers and with electrons bound at defects. However, for transitions between Kramers conjugate bound states its intensity is suppressed by a factor
 where
where 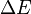 is the separation between adjacent levels of the orbital motion.
is the separation between adjacent levels of the orbital motion.Origin of high intensity of EDSR: Simplified theory and physical mechanism
As stated above, various mechanisms of EDSR operate in different crystals. The mechanism of its generically high efficiency is illustrated below as applied to electrons in direct-gap semiconductors of the InSb type. If spin-orbit splitting of energy levels is comparable to the forbidden gap
is comparable to the forbidden gap  , the effective mass of an electron
, the effective mass of an electron 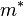 and its g-factor can be evaluated in the framework of the Kane scheme,[3][4] see [[
and its g-factor can be evaluated in the framework of the Kane scheme,[3][4] see [[ perturbation theory]]
perturbation theory]] ,
,where
 is a coupling parameter between the electron an valence bands, and
is a coupling parameter between the electron an valence bands, and  is the electron mass in vacuum.
is the electron mass in vacuum.Choosing the spin-orbit coupling mechanism based on the anomalous coordinate
 (see spin-orbit coupling) under the condition
(see spin-orbit coupling) under the condition  , we have
, we have
where
 is electron quasimomentum. Then energy of an electron in a ac electric field
is electron quasimomentum. Then energy of an electron in a ac electric field  is
is
An electron moving in vacuum with a velocity
 in an ac electric field
in an ac electric field  sees, according to the Lorentz transformation ab effective magnetic field
sees, according to the Lorentz transformation ab effective magnetic field  . Its energy in this field
. Its energy in this field
where
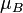 is the Bohr magneton and
is the Bohr magneton and  is the speed of light. The ratio of these energies
is the speed of light. The ratio of these energies .
.This expression shows explicitly where the dominance of EDSR over the electron paramagnetic resonance comes from. The numerator
 0.5MeV of the second factor is a half of the Dirac gap while
0.5MeV of the second factor is a half of the Dirac gap while  is of atomic scale,
is of atomic scale,  1eV.
The physical mechanism behind the enhancement is based on the fact that
inside crystals electrons move in strong field of nuclei, and in the
middle of the periodic table the product
1eV.
The physical mechanism behind the enhancement is based on the fact that
inside crystals electrons move in strong field of nuclei, and in the
middle of the periodic table the product  of the atomic number
of the atomic number 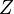 and the fine-structure constant
and the fine-structure constant  is of the order of unity, and it is this product that plays the role of the effective coupling constant, cf. spin-orbit coupling. However, one should bear in mind that the above arguments based on effective mass approximation are not applicable to electrons localized in deep centers of the atomic scale. For them the electron paramagnetic resonance is usually the dominant mechanism.
is of the order of unity, and it is this product that plays the role of the effective coupling constant, cf. spin-orbit coupling. However, one should bear in mind that the above arguments based on effective mass approximation are not applicable to electrons localized in deep centers of the atomic scale. For them the electron paramagnetic resonance is usually the dominant mechanism.Experiment
EDSR was first observed experimentally with free carriers in Indium antimonide (InSb), a semiconductor with strong spin-orbit coupling. Observations made under different experimental conditions allowed demonstrate and investigate various mechanisms of EDSR. In a dirty material, Bell[5] observed a motionally narrowed EDSR line at frequency against a background of a wide cyclotron resonance band. MacCombe et al.[6] working with high quality InSb observed isotropic EDSR driven by the
frequency against a background of a wide cyclotron resonance band. MacCombe et al.[6] working with high quality InSb observed isotropic EDSR driven by the  mechanism at the combinational frequency
mechanism at the combinational frequency  where
where  is the cyclotron resonance frequency. Strongly anisotropic EDSR band due to inversion-asymmetry
is the cyclotron resonance frequency. Strongly anisotropic EDSR band due to inversion-asymmetry  Dresselhaus spin-orbit coupling was observed in InSb at the spin-flip frequency
Dresselhaus spin-orbit coupling was observed in InSb at the spin-flip frequency  by Dobrowolska et al.[7] Spin-orbit coupling in n-Ge that manifests itself through strongly anisotropic electron g-factor results in EDSR through breaking translational symmetry by inhomogeneous electric fields
by Dobrowolska et al.[7] Spin-orbit coupling in n-Ge that manifests itself through strongly anisotropic electron g-factor results in EDSR through breaking translational symmetry by inhomogeneous electric fields  which mixes wave functions of different valleys.[8] Infrared EDSR observed in semimagnetic semiconductor Cd
which mixes wave functions of different valleys.[8] Infrared EDSR observed in semimagnetic semiconductor Cd Mn
Mn Se[9] was ascribed[10] to spin-orbit coupling
through inhomogeneous exchange field. EDSR with free and trapped charge
carriers was observed and studied at a large variety of
three-dimensional (3D) systems including dislocations in Si,[11] an element with notoriously weak spin-orbit coupling. All above experiments were performed in the bulk of three-dimensional (3D) systems.
Se[9] was ascribed[10] to spin-orbit coupling
through inhomogeneous exchange field. EDSR with free and trapped charge
carriers was observed and studied at a large variety of
three-dimensional (3D) systems including dislocations in Si,[11] an element with notoriously weak spin-orbit coupling. All above experiments were performed in the bulk of three-dimensional (3D) systems.Applications
Principal applications of EDSR are expected in quantum computing and semiconductor spintronics and are currently focused on low-dimensional systems. One of its main goals is fast manipulation of individual electron spins at a nanometer scale, e.g., in quantum dots of about 50 nm size. Such dots can serve as qubits of quantum computing circuits. Time-dependent magnetic fields practically cannot address individual electron spins at such a scale,
but individual spins can be well addressed by time dependent electric
fields
practically cannot address individual electron spins at such a scale,
but individual spins can be well addressed by time dependent electric
fields  produced by nanoscale gates. All basic mechanisms of EDSR listed above are operating in quantum dots,[12] but in A
produced by nanoscale gates. All basic mechanisms of EDSR listed above are operating in quantum dots,[12] but in A B
B compounds also the hyperfine coupling of electron spins to nuclear spins plays an essential role.[13][14][15] For achieving fast qubits operated by EDSR[16] are needed nanostructures with strong spin-orbit coupling. For the Rashba interaction
compounds also the hyperfine coupling of electron spins to nuclear spins plays an essential role.[13][14][15] For achieving fast qubits operated by EDSR[16] are needed nanostructures with strong spin-orbit coupling. For the Rashba interaction  the strength of interaction is characterized by the coefficient
the strength of interaction is characterized by the coefficient  . In InSb quantum wires the magnitude of
. In InSb quantum wires the magnitude of  of the atomic scale of about 1 eV
of the atomic scale of about 1 eV has been already achieved.[17]
A different way for achieving fast spin qubits based on quantum dots
operated by EDSR is using nanomagnets producing inhomogeneous magnetic
fields,[18] see Spin-orbit interaction.
has been already achieved.[17]
A different way for achieving fast spin qubits based on quantum dots
operated by EDSR is using nanomagnets producing inhomogeneous magnetic
fields,[18] see Spin-orbit interaction.
No comments:
Post a Comment